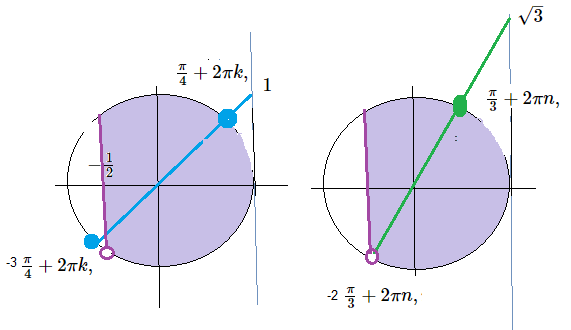Задача 46739 ...
Условие
б) [-π; π/2] .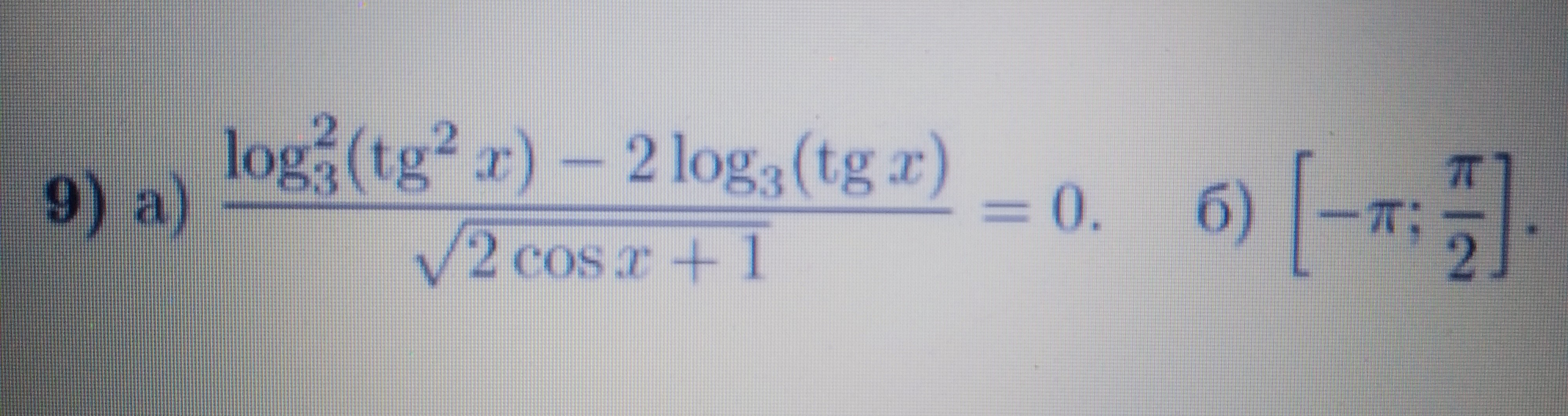
Решение
[m]\frac{log^{2}_{3}(tg^{2}x)-2log_{3}(tgx)}{\sqrt{2cosx+1}}=0[/m]
Дробь равна 0, когда числитель равен 0, а знаменатель отличен от 0
[m]\left\{\begin{matrix} log^{2}_{3}(tg^{2}x)-2log_{3}(tgx)=0\\ \sqrt{2cosx+1}\neq 0 \end{matrix}\right.[/m]
Подкоренное выражение не должно быть отрицательным,
выражение под знаком логарифма должно быть положительным, поэтому:
[m]\left\{\begin{matrix} log^{2}_{3}(tg^{2}x)-2log_{3}(tgx)=0\\tgx >0\\ 2cosx+1> 0 \end{matrix}\right.[/m]
При [m]tgx >0[/m] по свойству логарифма степени:
[m] log_{3}tg^{2}x=2log_{3}(tgx)[/m]
тогда
[m] log^2_{3}tg^{2}x=(log_{3}tg^{2}x)^{2}=(2log_{3}(tgx))^2=4log^{2}_{3}tgx[/m]
и
первое уравнение принимает вид:
[m]4 log^{2}_{3}(tgx)-2log_{3}(tgx)=0[/m]
Раскладываем на множители:
[m]\left\{\begin{matrix}2log_{3}(tgx)(2 log_{3}(tgx)-1)=0\\tgx >0\\ 2cosx+1> 0 \end{matrix}\right.[/m]
Произведение равно 0 тогда и только тогда когда хотя бы один из множителей равен 0, получаем совокупность двух систем:
[m]\left\{\begin{matrix}log_{3}(tgx)=0\\tgx >0\\ 2cosx+1> 0 \end{matrix}\right.\left\{\begin{matrix}2 log_{3}(tgx)-1=0\\tgx >0\\ 2cosx+1> 0 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}tgx=3^{0}\\tgx >0\\ 2cosx+1> 0 \end{matrix}\right.\left\{\begin{matrix} log_{3}(tgx)=\frac{1}{2}\\tgx >0\\ 2cosx+1> 0 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}tgx=1\\tgx >0\\ 2cosx+1> 0 \end{matrix}\right.\left\{\begin{matrix} tgx=3^{\frac{1}{2}}\\tgx >0\\ 2cosx+1> 0 \end{matrix}\right.[/m]
Корни в первой строке удовл второму неравенству
[m]\left\{\begin{matrix}tgx=1\\2cosx+1> 0 \end{matrix}\right.\left\{\begin{matrix} tgx=\sqrt{3}\\ 2cosx+1> 0 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}x=\frac{\pi}{4}+\pi k, k \in Z\\cosx>-\frac{1}{2} \end{matrix}\right.\left\{\begin{matrix}x=\frac{\pi}{3}+\pi n, n \in Z\\ cosx>-\frac{1}{2} \end{matrix}\right.[/m]
[m] cosx=-\frac{1}{2}[/m] ⇒ [m]x=\pm \frac{2\pi}{3}+2\pi m, m \in Z[/m]
Второму неравенству систем удовлетворяют корни только в первой четверти:
cм. рис.
[m]x=\frac{\pi}{4}+2\pi k, k \in Z[/m] или [m]x=\frac{\pi}{3}+2\pi n, n \in Z[/m]
О т в е т.
[m]\frac{\pi}{4}+2\pi k, k \in Z[/m] ; [m]\frac{\pi}{3}+2\pi n, n \in Z[/m]
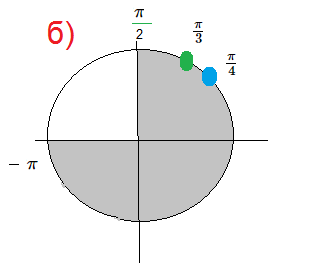
б)[m] \frac{\pi}{4} ; \frac{\pi}{3}[/m] - корни, принадлежащие указанному отрезку ( cм рис. б)