Задача 59614 Решить...
Условие
2sin^2x+1=2sqrt2sin(3pi/2+x)
Найти корни уравнения на промежутке: [17pi; 37pi/2]
математика 10-11 класс
2349
Решение
★
sin((3π/2)+x)=-cosx
Уравнение принимает вид:
2sin^2x+1=-2sqrt(2)cosx
sin^2x=1-cos^2x
2*(1-cos^2x)+1=-2sqrt(2)cosx
2cos^2x-2sqrt(2)cosx-3=0
D=(2sqrt(2))^2-4*2*(-3)=8+24=32
sqrt(32)=4sqrt(2)
cosx=-sqrt(2)/2 или сosx=3sqrt(2)/2
cosx=-sqrt(2)/2 ⇒ [b]x= ± (3π/4)+2πn, n ∈ Z[/b]
сosx=3sqrt(2)/2 - уравнение не имеет корней, так как
-1 ≤ сosx ≤ 1, 3sqrt(2)/2 >1
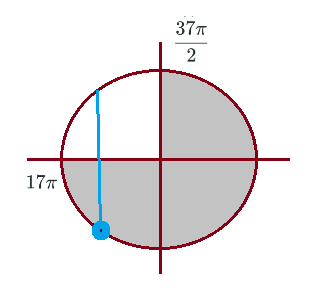
Отбор корней на единичной окружности:
см. рис.
x=-(3π/4)+18π=[b]69π/4[/b]
или
x=17π+(π/4)=[b]69π/4[/b]