Задача 63909 ...
Условие
б) Отбор корней на отрезке [2π; 7π/2] решить с помощью неравенства
Решение
sin((3π/2)–x)=-cosx
Уравнение можно записать в виде:
- (sin2x /cosx) = √2
-sin2x=√2cosx
cosx ≠ 0
-2sinx*cosx-√2cosx=0
cosx*(-2sinx-√2)=0
cosx ≠ 0
-2sinx-√2=0
sinx=-√2/2
a) О т в е т. (-1)^(k)(π/4)+πk, k ∈ Z
б) О т в е т. (-1)^(k)(π/4)+πk, k ∈ Z можно записать как две серии ответов
x=-(π/4)+2πn, n ∈ Z или x=-3π/4+2πn, n ∈ Z
Отбор корней с помощью неравенства:
2π ≤ -(π/4)+2πn ≤ 7π/2 ( делим на π)⇒ 2 ≤ -(1/4)+2n ≤ 7/2 ( умн на 4) ⇒ 8 ≤ -1+8n ≤ 14 ( прибавим 1)⇒
9 ≤ 8n ≤ 15
нет целых n, удовлетворяющих неравенству
2π ≤ -(3π/4)+2πn ≤ 7π/2 ( делим на π)⇒ 2 ≤ -(3/4)+2n ≤ 7/2 ( умн на 4) ⇒ 8 ≤ -3+8n ≤ 14 ( прибавим 3 )⇒
11 ≤ 8n ≤ 17
при n=2 неравенство верно: 11 ≤ 8*2 ≤ 17
x=-3π/4+2π*2=13π/4- корень принадлежащий указанному отрезку
О т в е т. б) 13π/4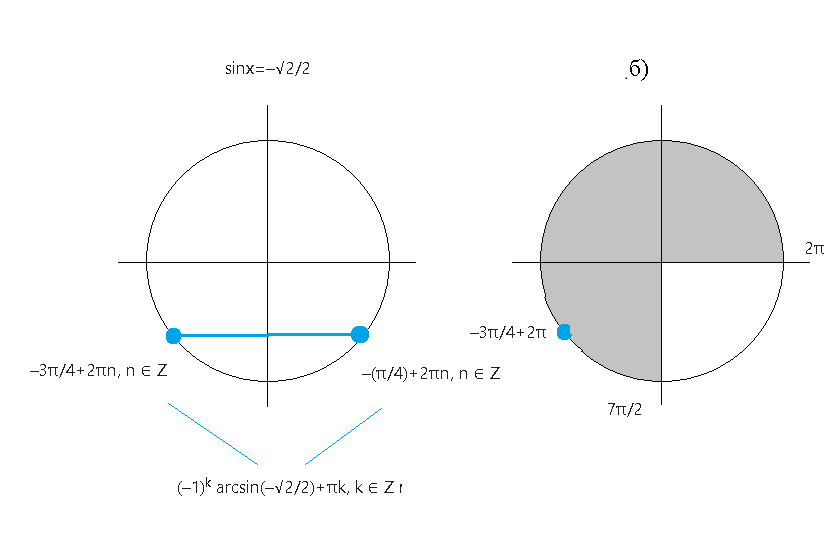
Все решения
