Эллипс, гипербола, парабола. СФЕРА

Найти на гиперболе x^2/2 - y^2 = 1 точку, ближайшую к точке (3,0) В ответе указать сумму модулей координат.

2. Написать каноническое уравнение эллипса, проходящего через
точку М(0; 4), если эксцентриситет его 3/5

3. Найти эксцентриситет гиперболы: ...

4. Найти уравнение директрисы параболы, симметричной
относительно оси Ох, проходящей через начало координат и точку ...

5. ...

Парабола проходить через точки (0;6)і(4;0) симетрично осі осі абсцис.напишіть її рівняння та побудуйте.

Запишите уравнение касательной к окружности(x+8)2+(y−3)2=68 в точке M0(0,1) в виде y=kx+d.
В ответ введите через точку с запятой значения:
k;d

С помощью выделения позднего квадрата привести заданное уравнение кривой второго порядка к каноническому виду. Определить тип кривой, найти ее полуоси, эксцентриситет, координаты вершин и фокусов, уравнения директрис и асимптот (если они имеются). Сделать чертеж.
3y-4x-2x^2-7=0

Составить уравнение окружности с центром в точке (1;4), проходящей через точку (3;5)

Написать уравнение окружности, если окружность проходит через точки М1 (-1;5) М2 (-2;-2) М3 (5;5) (тема:уравнение второго порядка, окружность)

Составить канонические уравнения: а) эллипса; б) гиперболы; в) параболы ( , AB
точки, лежащие на кривой, F - фокус, a - большая (действительная) полуось, b - малая
(мнимая) полуось,ƹ- эксцентриситет, y=±kx +b . . . - уравнения асимптот гиперболы, D -
директриса кривой, 2c - фокусное расстояние).
а) a=9, F(7, 0). ; б) b=6, F (12, 0). ; в) D: x=-1/ 4.

Гипербола касается прямых 5x – 6y – 16 = 0, 13x – 10y – – 48 = 0. Запишите уравнение гиперболы при условии, что ее оси совпадают с осями координат.

Привести уравнение линии второго порядка к каноническому виду и построить кривую: y^2-2x^2+8x-6=0

Определить полуоси, фокусы и уравнения асимптот гиперболы 4x^2-9y^2=25

Вычислить периметр и площадь равнобедренно треугольника с углом при основании 30градусов, если вершина его совпадает с вершиной параболы y^2=12x, а основание лежит на директрисе этой параболы

Записать уравнение окружности, проходящей через
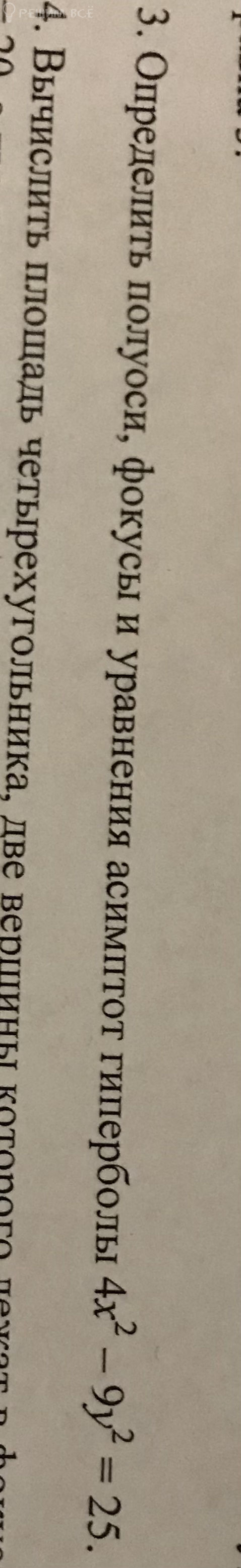
указанные точки и имеющий центр в точке A , сделать
рисунок
1. Вершины гиперболы
12x^2 -13y^2 = 156, А(0; 2)

Если бОльшая ось эллипса равна 8, а эксцентриситет равен 3, то левая директриса эллипса определяется уравнением

Составить канонические уравнения: а) эллипса; б) гиперболы; в) параболы (А, В - точки, лежащие на кривой, F - фокус, a - большая (действительная) полуось, b - малая (мнимая) полуось, - эксцентриситет, - уравнение асимптот гиперболы, D - директриса кривой, 2c - фокусное расстояние), если

а). ; б). k = 1/2, = , в). D: y = -1.

. Прямая l касается эллипса, фокусы которого расположены в точках F1,
F2. Составить каноническое уравнение этого эллипса и найти его l : x + 2y + 4 = 0, F1 = (−1, 0), F2 (1, 0).

Напишите каноническое уравнение гиперболы, зная, что ее асимптоты имеют уравнения y=±2x, а фокусное расстояние равно 10.

методом параллельных сечений исследовать поверхность.указать линию пересечения. сделать схематичный рисунок поверхностей и сечений. 4x+2y-z=0 четыре икс в квадрате плюс два игрик в квадрате минус зет в квадрате=0 а) y=1 б) x=0 в) z=0

Написать уравнение гиперболы, если известны ее асимптота у=2х и точка А(-2;0)

1. Составить канонические уравнения: а) эллипса; 6) гиперболы; в) параболы (А, В — точки, лежащие на кривой, Е — фокус, а — большая (действительная) полу- ось, В — малая (мнимая) полуось, & — эксцентриситет, у== + ёх — уравнения асимптот гиперболы, — — ди- ректриса кривой, 2с — фокусное расстояние).

Сфера задана уравнением x2 + y2 + z2 + 4x – 6y + 8 = 0.Найди координаты центра и радиус этой сферы.
Ответ округли до сотых долей.
Ответ: центр O(...;...;...);
радиус R = ...

составить уравнение эллипса с фокусами на оси абсцисс, если он проходит через точку(12,-12) и его большая ось =40

Найти координаты центра и радиус сферы, которая проходит через точки А(0;1;-1), B(1;0;1), C(-1;1;0), D(1;-1;1).

Вещественная ось гиперболы вертикальна и имеет длину 16, асимптоты гиперболы задаются уравнениями y=(3/4)x+4 и y=−(3/4)x−6. Найдите центр гиперболы, расстояние между её фокусами и её эксцентриситет.

Составить уравнение линии, каждая точка М которой, удовлетворяет заданным условиям.
Отстоит от прямой у = -2 на расстоянии, в три раза большем, чем от точки А (5,0)

Схематично изобразить поверхность и определить ее вид
а) х2=8(у2+z2); б) 2х2+3у2-z2=18; в) 2у2+5z2=10х; г) -5х2-3у2+4z2+60=0

Определить вид поверхности (название) и построить эту поверхность
a)-16x^2+y^2+4z^2-32=0
б)6x^2+y^2-3z^2=0

Составить каноническое уравнение гиперболы, если с=3, ε =1.5

Составить канонические уравнения: а) эллипса; 6) гиперболы; в) параболы. А, В — точки, лежащие на кривой; Ё — фокус; а — большая (действительная) полуось; Б — малая (мнимая) полуось; & — эксцентриситет; у = +Кх — уравнения асимптот гиперболы; О — директриса кривой; 2с — фокусное расстояние.

Построить кривые, заданные следующими уравнениями:
(x - 3)^2 + (y - 3)^2 = 4,
x^2/25 + y^2/49 = 1,
y^2/9 - x^2/36 = 1,
y^2 = -8x.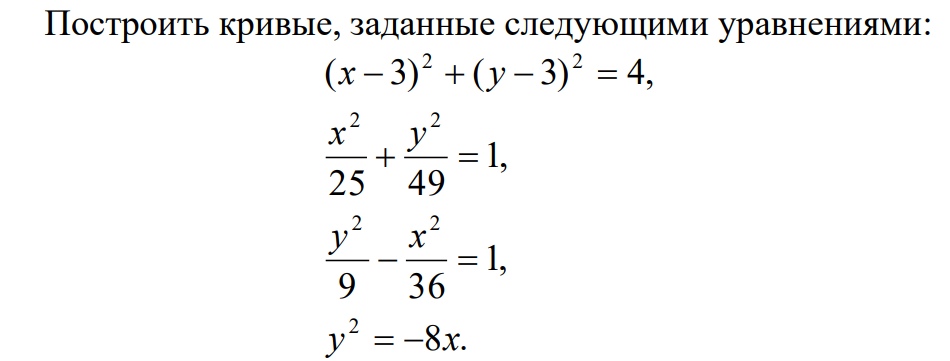

Записать уравнение и определить вид поверхности, полученной при вращении данной линии вокруг указанной оси координат. Сделать рисунок. -5х2+у2=5 вокруг оси Оy

составить уравнение эллипса зная что его фокусы находятся в точках a(8;2) и a(4;2) а длина малой полуоси равна 5

Записать уравнение окружности, проходящей через указанные точки и имеющей центр в точке А.

Составить каноническое уравнение эллипса фокусы которого лежат на оси ординат, симметрично относительно начала координат, зная что расстояние м/у его фокусами равно 2c = 6 и расстояние м/у директрисами равно 16 целых 2 /3





[green]Высшая математика[/green]

Задание 8

Найти координаты правого фокуса кривой
Координаты записать в строку ответа в соответствующем порядке через знак #.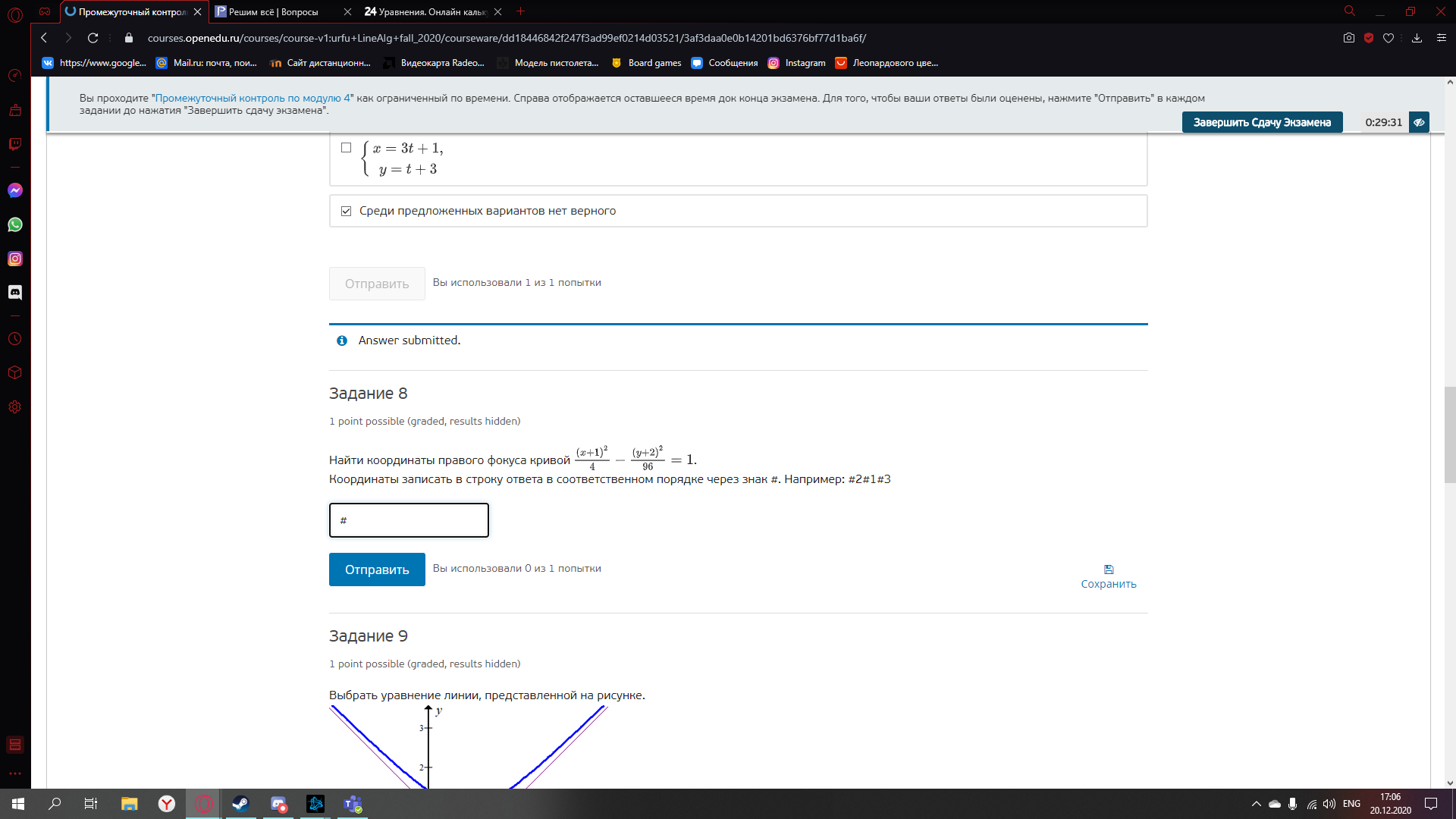

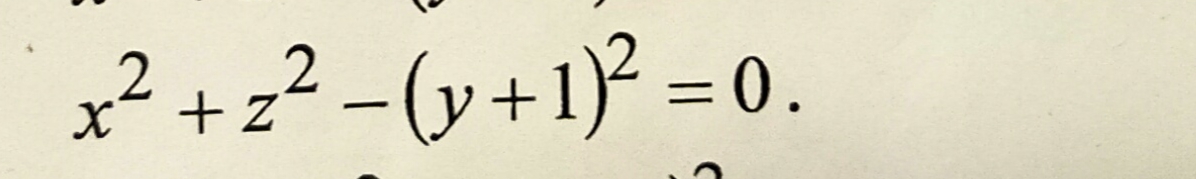
Определите вид поверхности, заданной уравнением. Выполните схематический чертеж. Составьте уравнение плоскости, проходящей через вершину этой поверхности. Постройте эту плоскость.

Привести уравнение линии второго порядка к каноническому виду.Назвать кривую, определяемую заданным уравнением и построить ее график
25 х^2+16у^2-200х+64у+64=о

Большая ось эллипса втрое больше его малой оси. Составить ка- ноническое уравнение этого эллипса, если он проходит через точку
M(3,√3). Сделать рисунок.

Найти эксцентриситает эллипса,если расстояние между его директрисами в три раза больше расстояния между фокусами.

С помощью выделения полного квадрата привести уравнение кривой второго порядка к каноническому виду. Определить тип кривой. Найти её полуоси, эксцентриситет, координаты вершин и фокусов, уравнения директрис и асимптот (если они имеются). Сделать чертеж. 4х^2-16х+5у+8=0

Выделить полные квадраты 2x²-12x-y+14=0
Должно получиться( x-3)²=1/2(y+4)
Но нужно расписать решение

оставить уравнение эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если даны:

1) точка М1(- 2√5; 2) эллипса и его малая полуось b = 3;

Найти центр и радиус окружности x^2+y^2-6x+2y-26=0

составить каноническое уравнение гиперболы имеющих общие фокальные хорды с эллипсом x^2/6+y^2/4=1

Составить каноническое уравнение парабол с фокусом F(0,-6) и F (2,0).

Составьте уравнение окружности с центром A и радиусом R.

а) A(7;11) R = 5
б) A(9; 4) R = 7
в) A(-2; 3) R = 1
г) A(-3; -4) R = 2

ПОМОГИТЕ ПОЖАЛУЙСТА
ПОДРОБНО
1)Напишите уравнение сферы с центром в начале координат, если плоскость y = 2 касается этой сферы.
2). Напишите уравнение сферы радиуса R = 4 с центром в точке А (-5; 7; 0);

ПОМОГИТЕ
1) Напишите уравнение сферы с центром в точке М ( 2;-3;4), и проходящей через точку С( 2; 0; 0).
2) Сфера задана уравнением (x-3)2+y2+(z+5)2 =9. Найдите значение m, при котором точка A(5;m;-3) принадлежит данной сфере.

ОЧЕНЬ СРОЧНО НАДО
1)Приведите данное уравнение к стандартному виду уравнения сферы и найдите координаты ее центра и радиус: х2+у2+z2+2y-4z=4.

Привести к каноническому виду, построить
кривую и найти ее характеристики:

Асимптоты гиперболы перпендикулярны, а отношение большего фокального радиуса точки M(−6;y) к меньшему радиусу этой же точки равно 3 + 2√2. Найти действительную и мнимую оси.

5. Определите вид кривой y²-4у+x=2, сделайте чертеж.

Найти множество точек, являющихся серединами хорд гиперболы

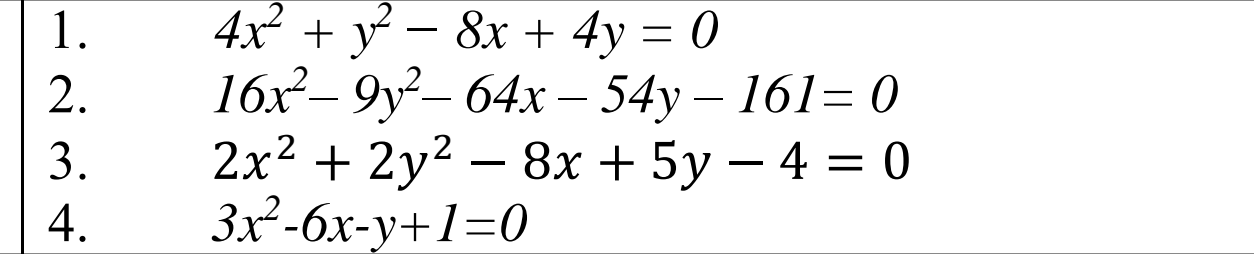
x^2 − 2 y^2 =1, параллельных прямой 2x − y = 0.Помогите пожалуйста,очень нужно.

Дано уравнение линии F(x, y) = 0. Построить линию, записав это уравнение в нормальной форме. Записать координаты фокусов. Если эта линия окажется параболой, то записать уравнение директрисы.

14. 4x^2 - 9y^2 -16x + 18y - 29 = 0.

Дана кривая 7y 2 +24xy+24x+62y+199 = 0.
Найдите координаты её центра симметрии.
Найдите действительную и мнимую полуоси.
Запишите уравнение фокальной оси.
Постройте данную гиперболу.

Найдите центр, вершины и фокусы каждого из приведённых ниже эллипсов.

(a) x^2/81 + y^2/25 = 1
Центр: ( , )
Правая вершина: ( , )
Левая вершина: ( , )
Верхняя вершина: ( , )
Нижняя вершина: ( , )
Правый фокус: ( , )
Левый фокус: ( , )

(b) (x + 17)^2/4 + (y - 8)^2/100 = 1
Центр: ( , )
Правая вершина: ( , )
Левая вершина: ( , )
Верхняя вершина: ( , )
Нижняя вершина: ( , )
Верхний фокус: ( , )
Нижний фокус: ( , )

(c) 9x^2 + 16y^2 - 72x - 192y + 576 = 0
Центр: ( , )
Правая вершина: ( , )
Левая вершина: ( , )
Верхняя вершина: ( , )
Нижняя вершина: ( , )
Правый фокус: ( , )
Левый фокус: ( , )

Вещественная ось гиперболы вертикальна и имеет длину 18, асимптоты гиперболы задаются уравнениями
[m] y = \frac{8}{3}x + 7y = -\frac{8}{3}x - 3 [/m]

Расстояние между фокусами гиперболы
Эксцентриситет равен

Установить, какую кривую определяет данное уравнение.
Найти:
1) координаты еѐ центра С;
2) полуоси;
3) координаты фокусов;
4) эксцентриситет;
5) уравнение директрисы;
6) уравнение асимптот (для гиперболы).
X2-4y2+6x+32y-119=0

с решением

Составить канонические уравнения: а) эллипса; б) гиперболы; в) параболы. A, B – точки, лежащие на кривой; F – фокус; a – большая (действительная) полуось; b – малая (мнимая) полуось; ε – эксцентриситет; D – директриса кривой; 2c – фокусное расстояние; у=+-kx(k=b/a) - уравнения асимптот гиперболы.
а) ε=7/8;А(8;0)
б)А(3;-sqrt(3/5);В(sqrt(3/5);6)
в)D:у=4

Уравнения линий привести к каноническому виду. Построить линии:

Изобразить линии:

Записать уравнение окружности проходящей через фокусы эллипса 3x^2+4y^2=12 и имеющей центр в точке A-его верхней вершине

Определить тип линии и найти ее основные характеристики [b]4x^(2)+3y^(2)-8x+12y-32=0[/b]

Вещественная ось гиперболы вертикальна и имеет длину 6, асимптоты гиперболы задаются уравнениями
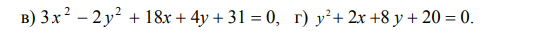
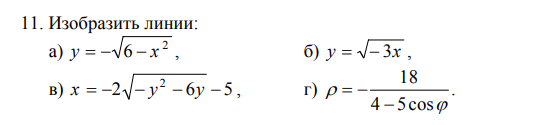
[m] y = \frac{5}{8}x - 2 [/m] и [m] y = -\frac{5}{8}x - 5 [/m]. Найдите центр гиперболы, расстояние между её фокусами и её эксцентриситет.

Найдите вершину, фокус и директрису для парабол, заданных следующими урвнениями.

(a)
[m](y - 7)^{2} = 4(x - 4)[/m]


вершина: ( , )

фокус: ( , )

директриса: [m]x =[/m]


(b)
[m]\ y^{2} - 8y = 20x - 4^{2}[/m]


вершина: ( , )

фокус: ( , )

директриса: [m]x =[/m]


(c)
[m](x - 1)^{2} = 20(y - 1)[/m]


вершина: ( , )

фокус: ( , )

директриса: [m]y =[/m]


(d)
[m]x^{2} + 8x = 4y - 28[/m]


вершина: ( , )

фокус: ( , )

директриса: [m]y =[/m]

Уравнение (x-2)^2/9 + (y-4)^2/25 = 1

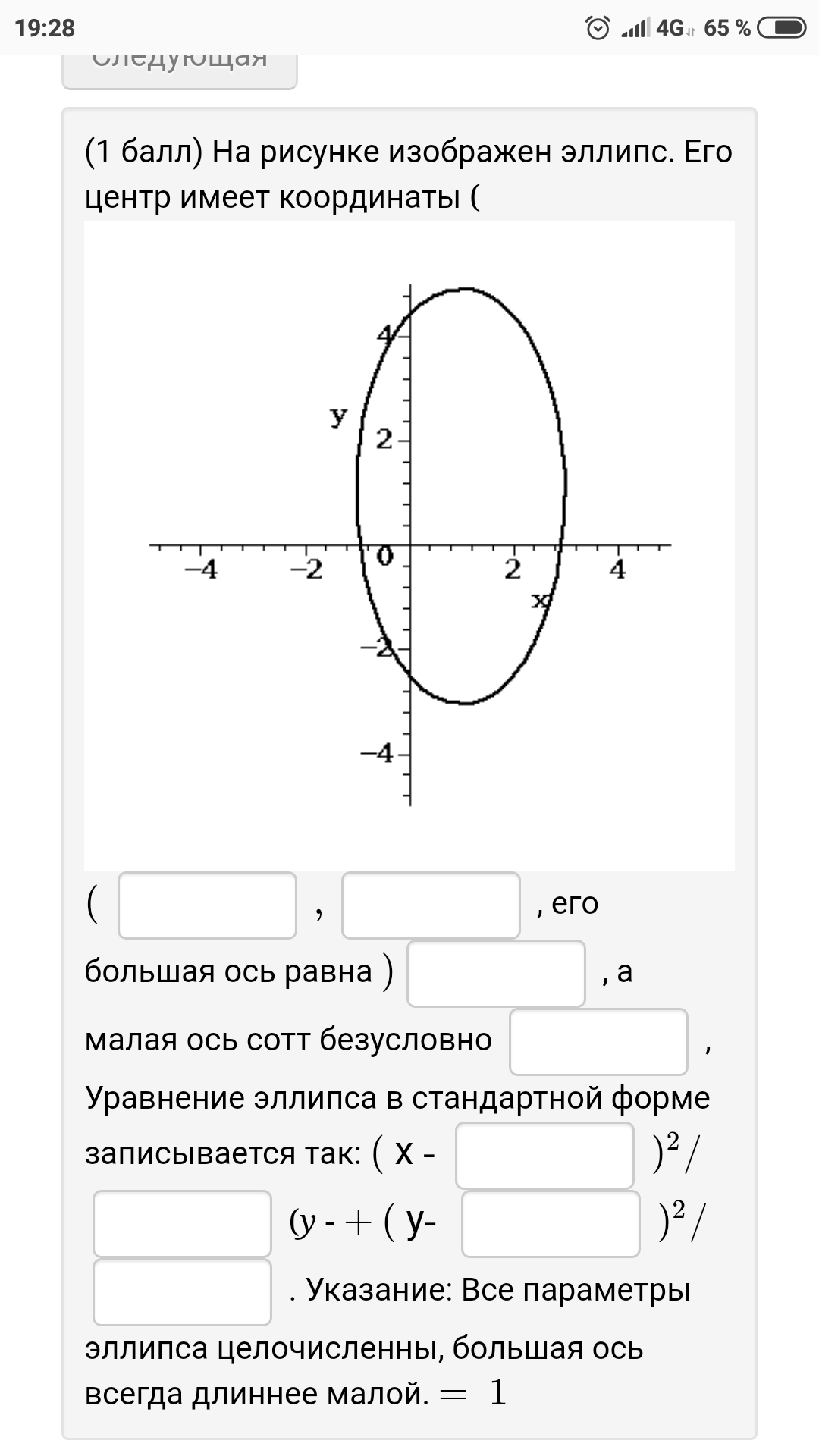
задает эллипс с центром в точке (______, ______). Тогда большая ось эллипса имеет длину ________, а малая ось - соответственно имеет длину ________.
Подсказка: Это уравнение в стандартной форме.

На рисунке изображен эллипс. Его центр имеет координаты

Здравствуйте нужна помощь;
№1 Cоставить каноническое уравнение гиперболы, если
а)2 с - 10, 2 а - 6;
b) c - 1,5, 2 c - 6;
№2 Даны гиперболы;
1) 16x^(2)-25y^(2)=400
№3 Определить координаты фокуса и составить уравнение директрисы каждой из парабол:
1) y^(2)=24x
2)y^(2)=-12x
3)x^(2)=4y
4)x^(2)=-32y

5. Найти параметрическое уравнение прямой.

Составить Каноническое уравнение: а) эллипса; б) гиперболы; в)
параболы (A, B – точки, Которые лежат на кривой, F – фокус, a – большая
(Действительная) полуось,
b – малая (мнимая) полуось,
ε – эксцентриситет,
y = ± kx – уравнения асимптот гиперболы,
D – директриса кривой,
2C – фокусное
расстояние).
а)ε= √21/5 ; A(–5;0)
б)A (√80;3) ,B(4 √6 ;3 √2) ;
в)D: y=1

Составить каноническое уравнение: а) эллипса; б) гиперболы; в) параболы. На фотографии вариант 14.6

Составить уравнение эллипса, зная, что:
а) его большая полуось равна 10 и фокусы суть F1(-6;0), F2(10;0)
б) а=5, F1(-3;5), F2(3;5)
2.
Составить каноническое уравнение эллипса, фокусы которого расположены на оси Ох, симметрично относительно начала координат, если:
а)задана точка M1(2 корня из 3;1) эллипса и его малая полуось равна 2
б) заданы две точки эллипса M1(0;7) и M2(8;0)
в)расстояние между фокусами равно 24 и большая ось равна 26
г) экцентриситет равен 7/25 и заданы фокусы (+-7;0)

Записать уравнение окружности, проходящей через указанные точки и имеющей центр в точке А.
Левую вершину гиперболы 5x^2–9y^2=45, A(0, –6)

Кривая второго порядка задана общим уравнением относительно ПДСК.

1) Привести уравнение к каноническому виду и построить линию;
2) найти координаты фокусов (фокуса – в случае параболы).

5х² + 12ху – 22х – 12у – 12 = 0

Составить канонические уравнения: а) эллипса; б)гиперболы; в) параболы. Где А, В – точки, лежащие на кривой, F – фокус, a – большая (действительная) полуось, b – малая (мнимая) полуось, Е – эксцентриситет, у = + –kx – уравнения асимптот гиперболы, D – директриса кривой, 2с –фокусное расстояние.
а) а=9, F(-10;0); б)b=6, F(12;0); в)D: x=-1/4

1. Дан треугольник АВС, в котором А(6;2), В (2;-3), С (-3;5). Составить уравнение медианы, проведённой из вершины А.

2. Дан эллипс x^2/49 + y^2/24 = 1. Найти эксцентриситет эллипса и его фокусы.

3. Составить уравнение прямой, проходящей через фокус параболы у^2 = 4х перпендикулярно к прямой х-3у+1=0

Создатель