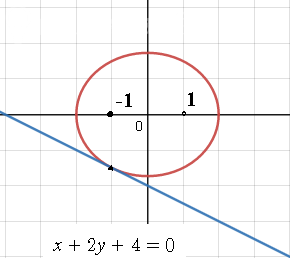
Задача 61549 . Прямая l касается эллипса, фокусы...
Условие
F2. Составить каноническое уравнение этого эллипса и найти его l : x + 2y + 4 = 0, F1 = (−1, 0), F2 (1, 0).
Решение
2c=2
[b]c=1[/b]
b^2=a^2-c^2 ⇒ a^2=b^2+c^2
c=1⇒[b] a^2=b^2+1[/b]
Так как даны координаты фокусов и фокусы симметричны относительно начала координат, то
каноническое уравнение эллипса имеет вид:
(x^2/a^2)+(y^2/b^2)=1
Пусть M - точка касания прямой х+2у+4=0 и эллипса
Эллипс симметричен относительно осей координат и относительно начала координат.
Значит , точка М лежит и на прямой перпендикулярной данной
Запишем уравнение данной прямой как уравнение прямой с угловым коэффициентом
y=-(1/2)x-2
Тогда уравнение перпендикулярной ей прямой, проходящей через начало координат
ее уравнение: [b]y=2x[/b]
Найдем координаты точки M как точки пересечения двух прямых:
{x+2y+4=0
{y=2x
x+2*2x+4=0
5x=-4
x=-0,8
y=2*(-0,8)=-1,6
M(-0,8; -1,6) подставляем координаты в уравнение эллипса
((-0,8)^2/a^2)+((-1,6)^2/b^2)=1
Решаем систему
{((-0,8)^2/a^2)+((-1,6)^2/b^2)=1
{[b] a^2=b^2+1[/b] ⇒
0,64b^2+2,56*(b^2+1)=b^2*(b^2+1)
b^4-2,2b^2-2,56=0
D=(-2,2)^2+4*2,56=4*(1,21+2,56)
b^2=