Задача 45010 ...

nast

2020-03-14 17:15:02

Асимптоты гиперболы перпендикулярны, а отношение большего фокального радиуса точки M(−6;y) к меньшему радиусу этой же точки равно 3 + 2√2. Найти действительную и мнимую оси.

sova

2020-03-18 19:42:02

Каноническое уравнение гиперболы:
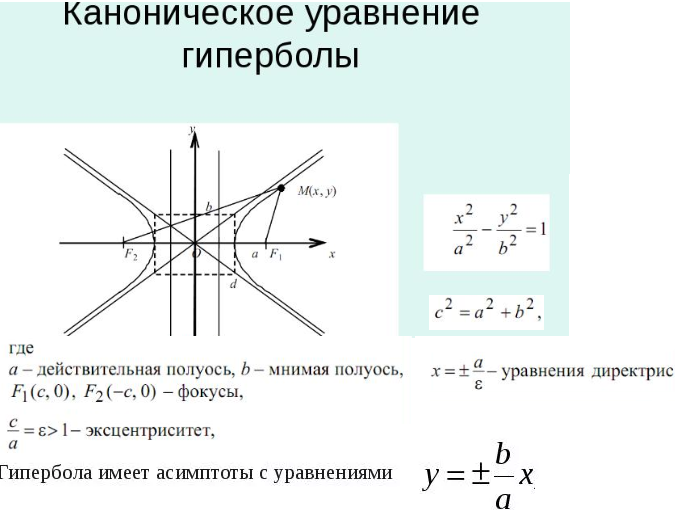
[m]\frac{x^2}{a^2}-\frac{y^2}{b^2}=1[/m]



Асимптоты гиперболы:
y= ± [m]\frac{b}{a}[/m]

По условию они перпендикулярны, значит произведение угловых коэффициентов равно (-1):

(b/a)*(-b/a)=-1 ⇒ b^2=a^2 ⇒ b=a

т. е уравнение гиперболы имеет вид:

x^2-y^2=a^2

b^2=c^2-a^2

a=b ⇒ c^2=2a^2

c=a*sqrt(2)
ε =с/a=sqrt(2)- эксцентриситет гиперболы.

r_(2)=F_(1)M=sqrt((-6-c)^2+y^2)
r_(1)=F_(2)M=sqrt((-6+c)^2+y^2)

r_(2):r_(1)=3+2sqrt(2)