Задача 32982 Вещественная ось гиперболы вертикальна и...

vk151256823

24 января 2019 г. в 08:08

Вещественная ось гиперболы вертикальна и имеет длину 6, асимптоты гиперболы задаются уравнениями
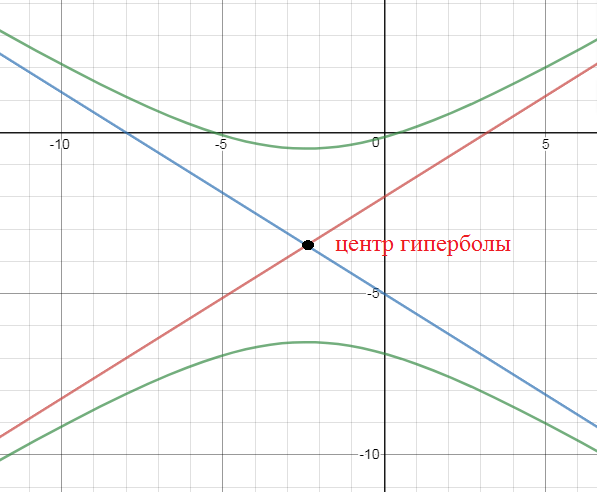
[m] y = \frac{5}{8}x - 2 [/m] и [m] y = -\frac{5}{8}x - 5 [/m]. Найдите центр гиперболы, расстояние между её фокусами и её эксцентриситет.

sova

24 января 2019 г. в 12:40

★

Находим координаты точки пересечения асимптот.
(5/8)х – 2 = (–5/8)х – 5;
(10/8)х=–3
х=–24/10=–2,4
y=–3,5
(–2,4; –3,5)– центр гиперболы

Вещественная ось вертикальна,
2b=6
b=3.
Из уравнения асимптот
5/8=3/a
a=24/5

значит уравнение гиперболы

(х–(–2,4))²/(24/5)² – (y–(–3,5))²/3² = –1


c²=a²+b²=(576/25)+9=(576+225)/25=(801)/25
c=√801/5

Расстояние между фокусами
2с=2√801/5

Эксцентриситет
ε=с/b=√801/(5·3) ≈ 1,88679622641