Задача 32163 Составить каноническое уравнение: а)...
Условие

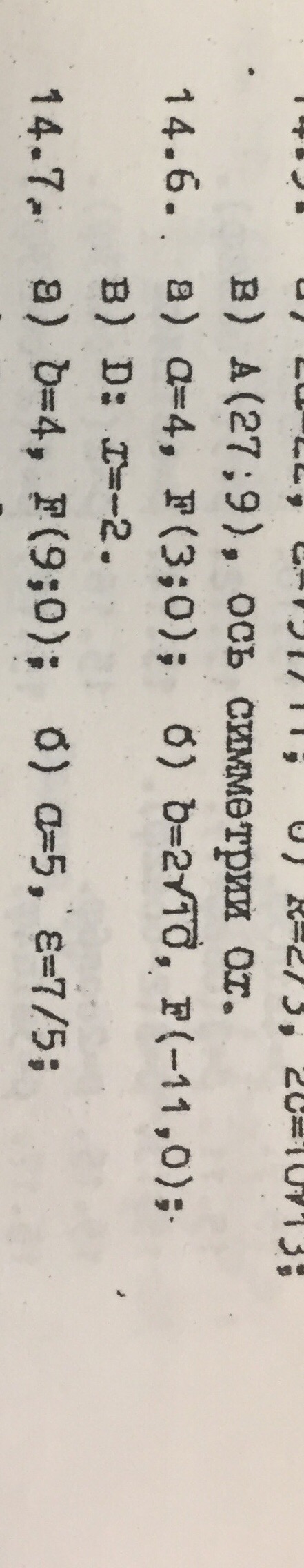
математика ВУЗ
2668
Решение
★
a=4
F(3;0) ⇒ c=3
b^2=a^2-c^2=4^2-3^2=7
Каноническое уравнение эллипса:
(x^2/a^2)+(y^2/b^2)=1
О т в е т.
(x^2/16)+(y^2/7)=1
б)
b=2sqrt(10) ⇒ b^2= 40
F(-11;0) ⇒ c=11
a^2=c^2-b^2=121-40=81
Каноническое уравнение гиперболы
(x^2/a^2)-(y^2/b^2)=1
О т в е т. (x^2/81)-(y^2/40)=1
в)D: x= - 2
если каноническое уравнение параболы имеет вид
y^2=2px, то фокус параболы
F(p/2;0)
D: x= - p/2
Значит,
p/2=2
p=4
О т в е т. y^2 = 8x