Задача 62271 Записать уравнение окружности,...

61bee639293da3503183e168

19.12.2021 10:59:44

Записать уравнение окружности, проходящей через
указанные точки и имеющий центр в точке A , сделать
рисунок
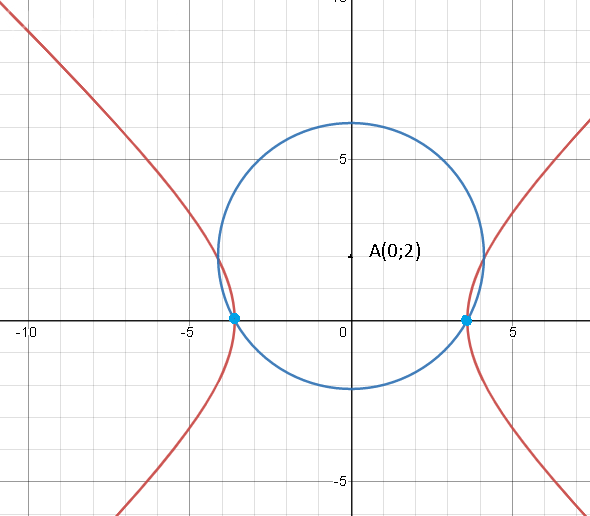
1. Вершины гиперболы
12x^2 -13y^2 = 156, А(0; 2)

5f3ea7e3faf909182968ddd9

19.12.2021 11:16:28

★

12x^2 –13y^2 = 156

Делим на 156

(x^2/13)-(y^2/12)=1- каноническое уравнение гиперболы с действительной осью Ох

Значит вершины гиперболы в точках

(-sqrt(13);0) и (sqrt(13);0)


Каноническое уравнение окружности с центром в
А(0; 2)

(x-0)^2+(y-2)^2=R^2

Подставляем координаты вершин гиперболы:

(-sqrt(13);0) ((-sqrt(13)^2-0)^2+(0-2)^2=R^2 ⇒ R^2=13+4=17

и (sqrt(13);0)((sqrt(13)^2-0)^2+(0-2)^2=R^2 ⇒ R^2=13+4=17

О т в е т. (x-0)^2+(y-2)^2=17 или [b] x^2+(y-2)^2=17[/b]