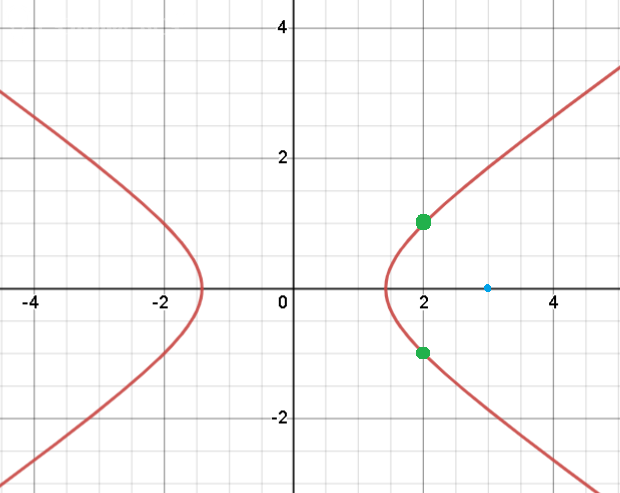
Задача 74792 Найти на гиперболе x^2/2 - y^2 = 1...

657c759442718a6f375fdf09

12/15/2023 3:50:41 PM

Найти на гиперболе x^2/2 - y^2 = 1 точку, ближайшую к точке (3,0) В ответе указать сумму модулей координат.

5f3ea7e3faf909182968ddd9

12/15/2023 7:36:14 PM

★

Пусть M(x; ±[m] \sqrt{\frac{x^2}{2}-1}[/m])- точка на гиперболе

N(3;0)

MN^2=(3-x)^2+(0-(±[m] \sqrt{\frac{x^2}{2}-1})[/m])^2=[m]9-6x+x^2+\frac{x^2}{2}-1[/m]

MN=[m]\sqrt{9-6x+x^2+\frac{x^2}{2}-1}=\sqrt{\frac{3x^2}{2}-6x+8}[/m]

MN - принимает наименьшее значение, когда квадратный трехчлен принимает наименьшее значение

А квадратный трехчлен ( график парабола, ветви вверх) принимает наименьшее значение в вершине параболы

т.е в точке x=[b]2[/b]

[m]y=± \sqrt{\frac{x^2}{2}-1}=± \sqrt{\frac{2^2}{2}-1}= ± 1[/m] ( две точки, см рис) (2;1) и (2;-1)


Сумма модулей координат точки:

2+1=3