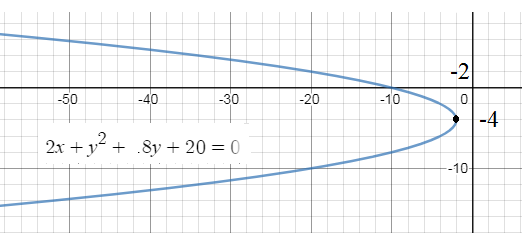Задача 41737 Уравнения линий привести к каноническому...
Условие
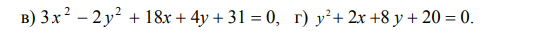
математика ВУЗ
929
Решение
★
3*(x^2+6x+9)-27-2*(y^2-2y+1)+2+31=0
3*(x+3)^2-2*(y-1)^2=-4
Делим на (-4)
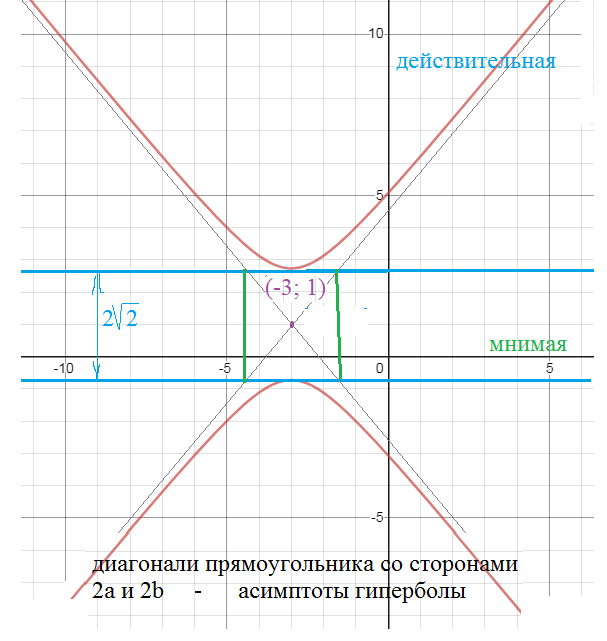
((y-1)^2/2)-((x+3)^2/(4/3))=1 - гипербола, центр в точке (-3; 1)
большая полуось - на оси, параллельной оси Оу
равна b= sqrt(2)
малая полуось - на оси, параллельной оси Ох
равна a= sqrt(4/3)
2)
2x+(y^2+8y)+20=0
2x+(y^2+2*y*4+16)-16+20=0
2x=-(y+4)^2-61
x=-(1/2)(y+4)^2-2 - парабола вдоль оси Ох
ветви в направлении противоположном направлению оси Ох
Вершина в точке (-4;-2)