Задача 41920 1. Дан треугольник АВС, в котором...

vk204612882

26 ноября 2019 г. в 10:20

1. Дан треугольник АВС, в котором А(6;2), В (2;–3), С (–3;5). Составить уравнение медианы, проведённой из вершины А.

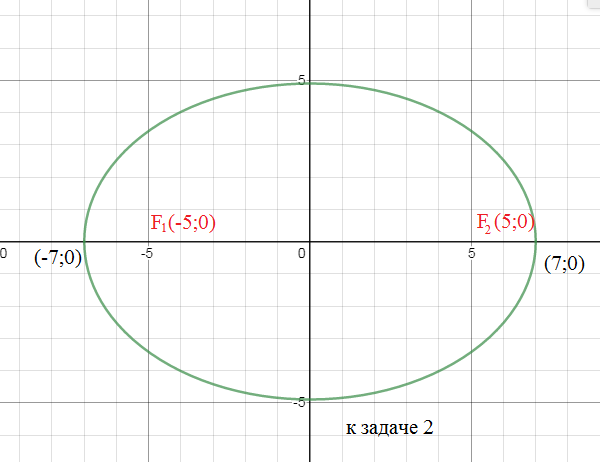
2. Дан эллипс x²/49 + y²/24 = 1. Найти эксцентриситет эллипса и его фокусы.

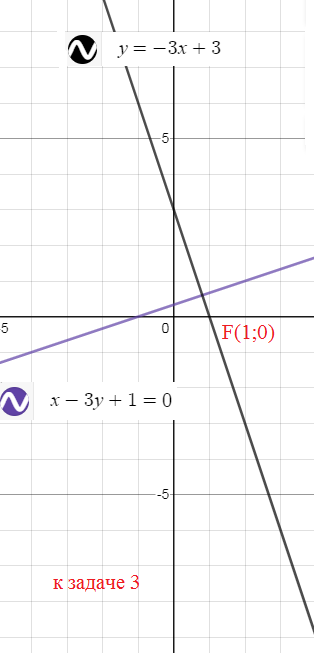
3. Составить уравнение прямой, проходящей через фокус параболы у² = 4х перпендикулярно к прямой х–3у+1=0

sova

26 ноября 2019 г. в 14:47

★

1.
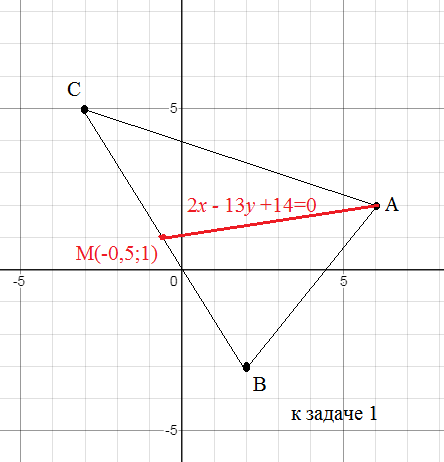
Точка M – середина ВC
x_M=[m]\frac{x_{B}+x_{C}}{2}[/m]
y_M=[m]\frac{y_{B}+y_{C}}{2}[/m]

x_M=[m]\frac{2+(-3)}{2}=-0,5[/m]
y_M=[m]\frac{-3+5}{2}=1[/m]


M(–0,5;1)

Уравнение AМ, как уравнение прямой проходящей через две точки:
[m]\frac{x-x_{A}}{x_{M}-x_{A}}=\frac{y-y_{A}}{y_{M}-y_{A}}[/m]

[m]\frac{x-6}{-0,5-6}=\frac{y-2}{1-2}[/m]

Умножаем обе части на (–13):

2·(x–6)=13·(y–2)

2х–13у+14=0 – уравнение медианы AМ

2.
Каноническое уравнение эллипса
[m]\frac{x^2}{a^2}+\frac{y^2}{b^2}=1[/m]

с²=a²–b²

[m]\frac{x^2}{49}+\frac{y^2}{24}=1[/m]

a²=49
b²=24

c²=a²–b²=49–24=25

с=5

Эксцентриситет
ε =с/а=5/7

3.
Каноническое уравнение параболы:
y²=2px
F(p/2;0)

y²=4x ⇒ 2p=4 ⇒ p=2

F(1;0)

Произведение угловых коэффициентов взаимно перпендикулярных прямых
k₁·k₂=–1

x–3y+1=0 запишем в виде y=[m]\frac{1}{3}x+\frac{1}{3}[/m]

k₁=[m]\frac{1}{3}[/m]

k₂=–3

Общий вид прямых перпендикулярных прямой x–3y+1=0

y=–3x+b

Прямая проходит через фокус параболы, т.е через точку F(1;0)

Подставляем координаты точки F:

0=–3·1+b

b=3

О т в е т. y=–3x+3