Аналитическая геометрия

Составить уравнение прямой, плоскости, найти угол между прямыми

3.4.2 Проверить компланарны ли векторы a=j+k , b=j–k , c=i

Даны вершины АВС: А(1,2,–1), B(3,4,0), C(2,5,–2).
Найти внутренний угол при вершине А.

Составить уравнение прямых АВ и АС если А(1,–2,1) В(0,–2,5) С(–1, – 1,1)

Составить уравнение прямой, проходящей через точку Мо(1,1):

а) параллельно прямой l: х+2у+2=0;

б) перпендикулярно прямой l: х+2у+2 =0.

Даны вершины треугольника А(– 8;—2), В(2;10), С(4;4) Найти
а) уравнение высоты, проведенной из вершины А;

6) уравнение медианы, проведенной из вершины С;

в) угол В.

Составить уравнение плоскости АВС ЕСЛИ А(1,–2, 1) В(0,2,5) С(–1,–1,1)

Найти расстояние от точки D до плоскости ABC ЕСЛИ А(1,–2, 1) В(0,2,5) С(–1,–1,1)

Даны точки А(3,0,–3), B(1,2,3), C(2,–2.1). Вычислить площадь треугольника АВС.

Найти середину отрезка AB, если A(7; 3; –3), B (3; –1; 1).

1. Найти частные производные второго порядка: z = (y–2)/x².

2. Найти экстремумы функции двух переменных:
z = 2x³ + 6xy² – 30x – 24y + 9.

3. Найти указанные производные z = 3x³ + xy² – 5xy³ – 2x + y, ∂4z ∂x∂y3 = ?

4. Найти наибольшее и наименьшее значения функции z = x2 – xy + y2 – 4x в треугольнике x = 0, y = 0, 2x + 3y – 12 = 0.

5. Найти точку пересечения прямой и плоскости
x–5 –2 y–2 0 z+4 –1 2x – 5y + 4z + 24 = 0.

Даны точки М(–2;2)и Р (2;10) найдите координаты точки К которая делит отрезок МР в отношении 1:4 считая от очки п

Какие из точек А(3,–1,–1), В(1,2,7), С(–5,14,–3) принадлежат прямой х=1+t,
y=2–3t, z=7–8t ???

Найти координаты точки пересечения плоскости, проходящей через точки A=(–4;4;–4), B=(4;0;–6), C=(–8;7;–2) c прямой, проходящей через точки D=(–22;12;–2), E=(–30;20;6).

Дано точки А(1;0;0), B(x;0;2), C(1;2;2). При яких значеннях x трикутник ABC є рівностороннім?

Середина відрізка MN належить осі ординат. Знайдіть a і b, якщо:
а) M(a;–1;–3), N(–2;9;b);
б) M(a–b;–3;–4), N(–1;7;a+2b)

На відрізку AB позначено точку M так, що AM:MB=1:3. Знайдіть координати:
а) точки M, якщо A(–7;4;0), B(5;0;–8);
б) точки B, якщо A(2;–9;6), M(1;–6;4).

1. Составить уравнение прямой, если известно, что точка Р (2;3) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.

2. Даны два вектора: а= (3;–1;5), b= (1;2;–3) . Найти вектор при условии, что он перпендикулярен к оси OZ и удовлетворяет условиям: xa=9, xb=4.
3. Найти координаты точки, симметричной точке (2;–4), относительно прямой 4x+3y+1=0.

Найти множество точек, являющихся серединами хорд гиперболы

x² − 2 y² =1, параллельных прямой 2x − y = 0.Помогите пожалуйста,очень нужно.

Написать уравнение плоскости, проходящей через прямую (x–0,5)/(–2) = (y+3)/1 = (z+2,5)/3 и перпендикулярной к плоскости 3x+4y–5z–6 = 0

Составить уравнение плоскости, проходящей через точку A(3,4,0) и прямую

(x–2)/1 = (y–3)/2 = (z+1)/2

Даны координаты вершины А( 2, 5) треугольника АВС и уравнения высот ВН: – 3х – 3у –12 = 0 и СК: х + 10у – 19 = 0. Найти координаты вершины В.

Найти расстояние от точки Q(0; 2) до прямой, проходящей через
точки А(5; –2) и В(3; 1).

Даны вершины треугольника ABC. Найти: а) уравнение стороны AB; б) уравнение высоты CH; в) уравнение медианы AM; г) точку персечения медианы AM и высоты CH; д) уравнение прямой, проходящей через вершину C параллельно стороне AB; е) расстояние от точки C до прямой AB
A(–1,–4); B(9;6); C(–5,4)

В−I

Треугольник задан вершинами
А(–6;–2), В(4;8 ), С(2;– 8)
Найти

1) Уp–е прямой (BN)|| (АС)
2) Уp–е медианы (CD)
3) Уp–е высоты
4) Угол В
5) Центр тяжести

1. Составить уравнение прямой проходящей через т. А перпендикулярно вектору: n=2i+3j.
2. Вычислите угол между двумя прямыми. 8x+4y–4=0 и
3. x+2y–5=0.
4. Составить уравнение прямой проходящей через т.А (2;3) и параллельно прямой:
x–1 / 3 = y+2 / 2
5. Дан треугольник ABC: А(1;2), В(4;1), С(0;2). Составить уравнение высоты АН. В каком расположении находятся прямые 2x–y+9=0 и x+2y–1=0.

1. Дан треугольник АВС, в котором А(6;2), В (2;–3), С (–3;5). Составить уравнение медианы, проведённой из вершины А.

2. Дан эллипс x²/49 + y²/24 = 1. Найти эксцентриситет эллипса и его фокусы.

3. Составить уравнение прямой, проходящей через фокус параболы у² = 4х перпендикулярно к прямой х–3у+1=0

Составить уравнения сторон треугольника, зная одну его вершину A(3;–1), а также уравнения биссектрисы x–4y+10=0 и медианы 6x+10y–59=0, проведенных из различных вершин.

Найти уравнение сторон треугольника, если известны одна из вершин В(–2;–4) и уравнение медианы 2х–5у+8=0 и высоты х+2у–14=0 проведеденных из этой вершины

Найти угол между ребрами АB и АD. На кооридинаты вершин пирамиды A(1:–2:1) B(3:1:–2) C(2:2:5) D(–2:1:0)

Помогите пожалуйста решить за ранее спасибо

1)Составить уравнение прямой проходящей через начало координат под углом в 30 ° к положительно направлению оси OX.

√3x + 3y = 0 ; 3x – √3y = 0 ; √3x – 3y = 0
2)Составить уравнение прямой L проходящей через две точки A(–2;3) и B(5;3)

y=3 ; y+3=0 ; 2x–5y=3=0
3)Указать угловой коэффициент и начальную ординату прямой 4x–3y+9=0.

k=4/3 b=3 ; k=3/4 b=–9/4 ; k=4 b=9
4)Указать координаты середины длинны отрезка AB, где A и B точки пересечения прямой 2x–y+4=0 с осями координат.

(2;2) ; (–1;2) ; (2;–1)
5)Составить уравнение прямой L, которая параллельна оси OY и проходит через центр тяжести треугольника ABC

A(–2;5) B(4;1) C(10;0)

y=7 ; 3x+2y=0 ; x=4

Составить параметрическое уравнение и построить прямую, подходящую через т.М0 параллельно вектору α , если:
М0(0;1), α (1;0)

Составить уравнение плоскости Р, проходящей через точку А
перпендикулярно вектору

BC
. Написать ее общее уравнение, а также
нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить
уравнение плоскости
P1
, проходящей через точки А, В, С. Найти угол между
плоскостями Р и
P1
. Найти расстояние от точки D до плоскости Р
А(1;1;2) В(2;3;–1) С(2;–2;4) D(–1;2;2)

Прямая l задана в пространстве общими уравнениями. Написать её каноническое и параметрическое уравнения. Составить уравнение прямой 1 l, проходящей через точку М параллельно прямой l, и вычислить расстояние между ними. Найти проекцию точки М на прямую l и точку пересечения прямой l и плоскости Р.
Общие уравнения прямой l
2x–3y–2z+6=0
x–3y+z+3=0
Координаты точки М (0;2;–1)
Общее уравнение плоскости Р x–2y+3z–4=0

Прямая задана координатно–параметрическими уравнениями
[m] x = 1 + 5t, y = 2 + 2t, z = 3 + 4t. [/m]
Вторая прямая параллельна первой и проходит через точку [m] P(-3, 5, 1) [/m].

Найдите точки пересечения второй прямой с координатными плоскостями: с плоскостью [m] xy [/m]: , с плоскостью [m] xz [/m]: , с плоскостью [m] yz [/m]:.

Запишите общее уравнение плоскости, в котором коэффициент при переменной x равен 11, если известно, что плоскость проходит через три точки (–5, –3, –1), (–2, 0, –6), (–2, 1, –4).

Найдите объем косоугольного параллелепипеда с ребрами PQ, PR, PS, если P(–1, 3, –3), Q(1, 6, 0), R(–2, 2, –4), S(5, 1, –1).

Помогите пожалуйста решить задачу !!!

Найдите векторно–параметрическое уравнение и координатно–параметрические уравнения прямой линии, проходящей через точки [m] P(3, 1, -4) [/m] и [m] Q(7, 0, -7) [/m].

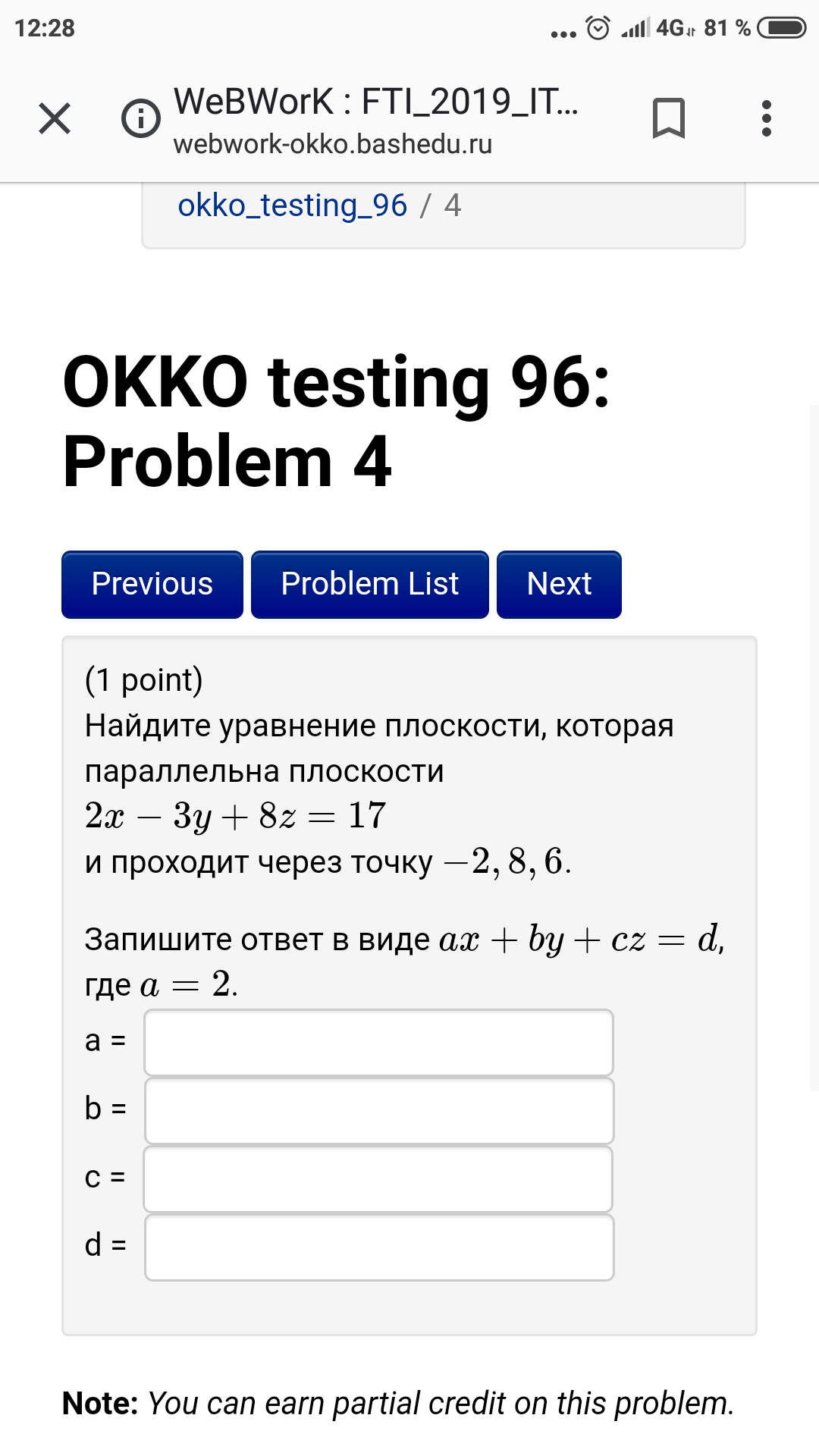
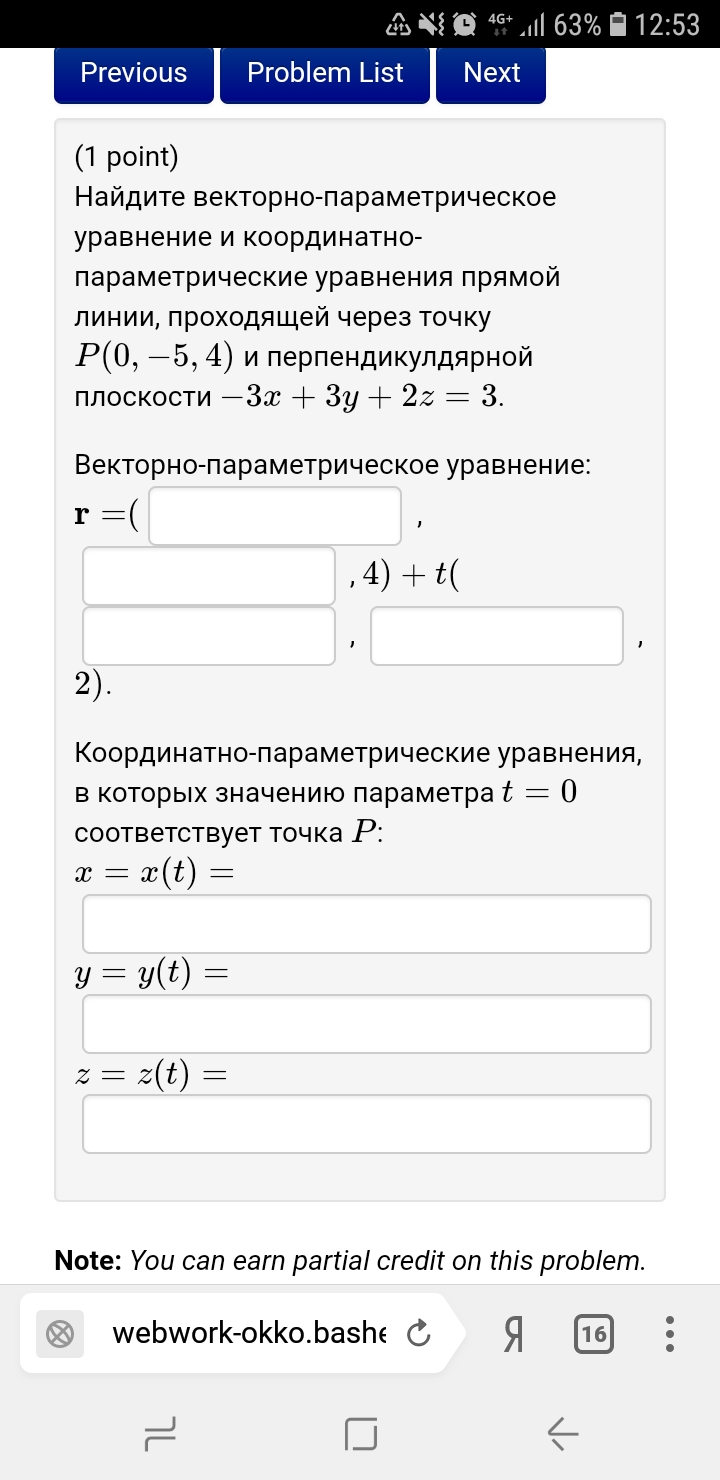
Векторно–параметрическое уравнение:

[m]
\mathbf{r} = \left( \begin{array}{c} \\ \\ \end{array} \right) + t \left( \begin{array}{c} \\ \\ \end{array} \right)
[/m]

Координатно–параметрические уравнения, в которых значению параметра [m] t = 0 [/m] соответствует точка [m] P [/m]:

[m]
x = x(t) =
[/m]

[m]
y = y(t) =
[/m]

[m]
z = z(t) =
[/m]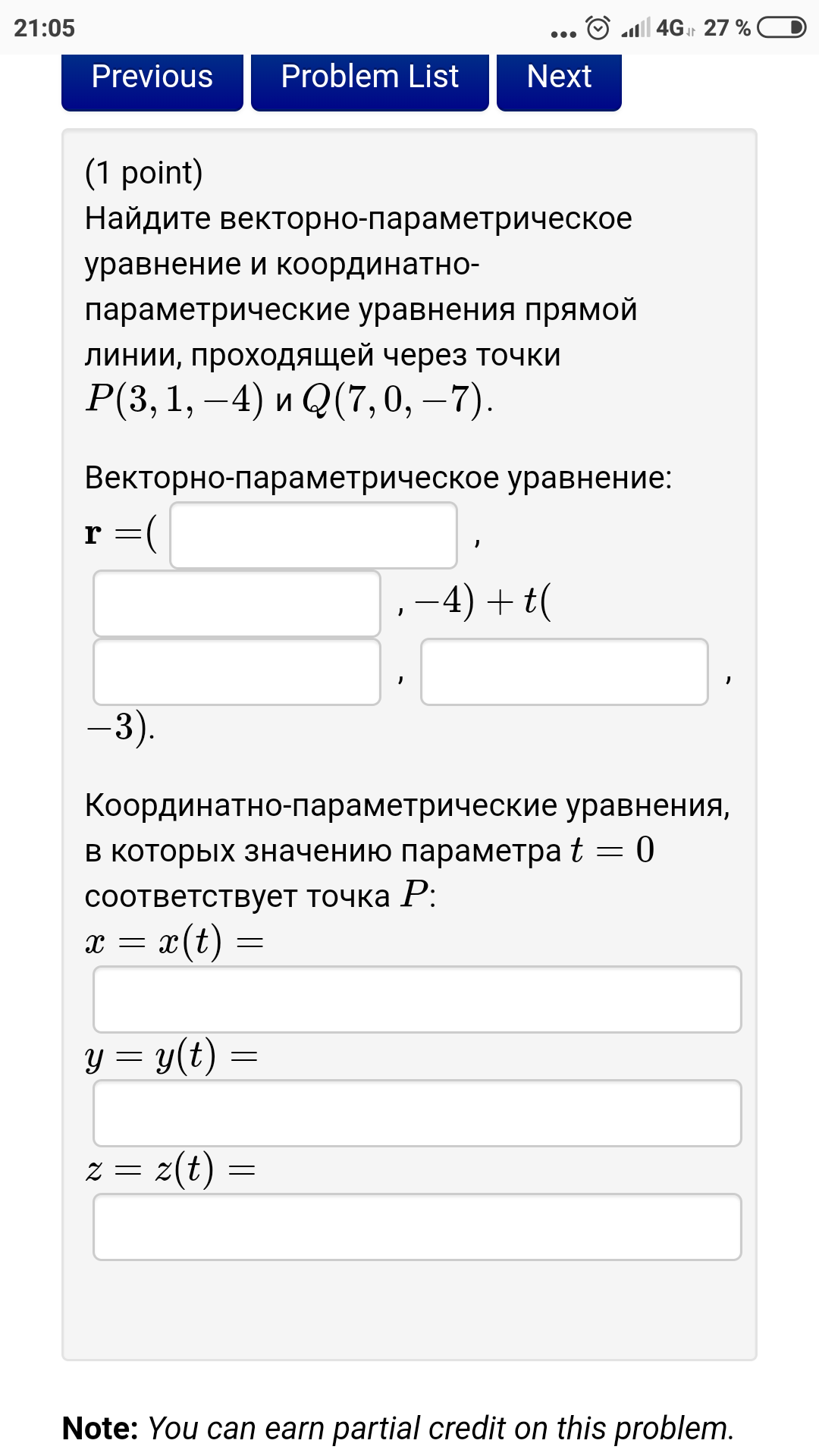

Найдите расстояние от точки (5, –5, –2) до плоскости 1x – 3y + 5z = 4.

Найдите векторно–параметрическое уравнение прямой линии, получающейся в пересечении двух плоскостей
5x + 2y – z = –5 и 5x + 3z = 2.

r = ( , , 0) + t(6, , ).

Даны три точки
(–3, 1, –1) (–8, 5, 0) (–8, 6, 2)

Найдите вектор нормали к этой плоскости, который имеет вид (–7 ____, ____ )

Найдите векторно–параметрическое уравнение прямой линии, получающейся в пересечении двух плоскостей
3x – 5y + 5z = – 2 и 3x + 3z = – 1.

Найдите векторно–параметрическое уравнение и координатно–параметрические уравнения прямой линии, проходящей через точки P(1, 5, 4) и Q(–2, 4, 1).

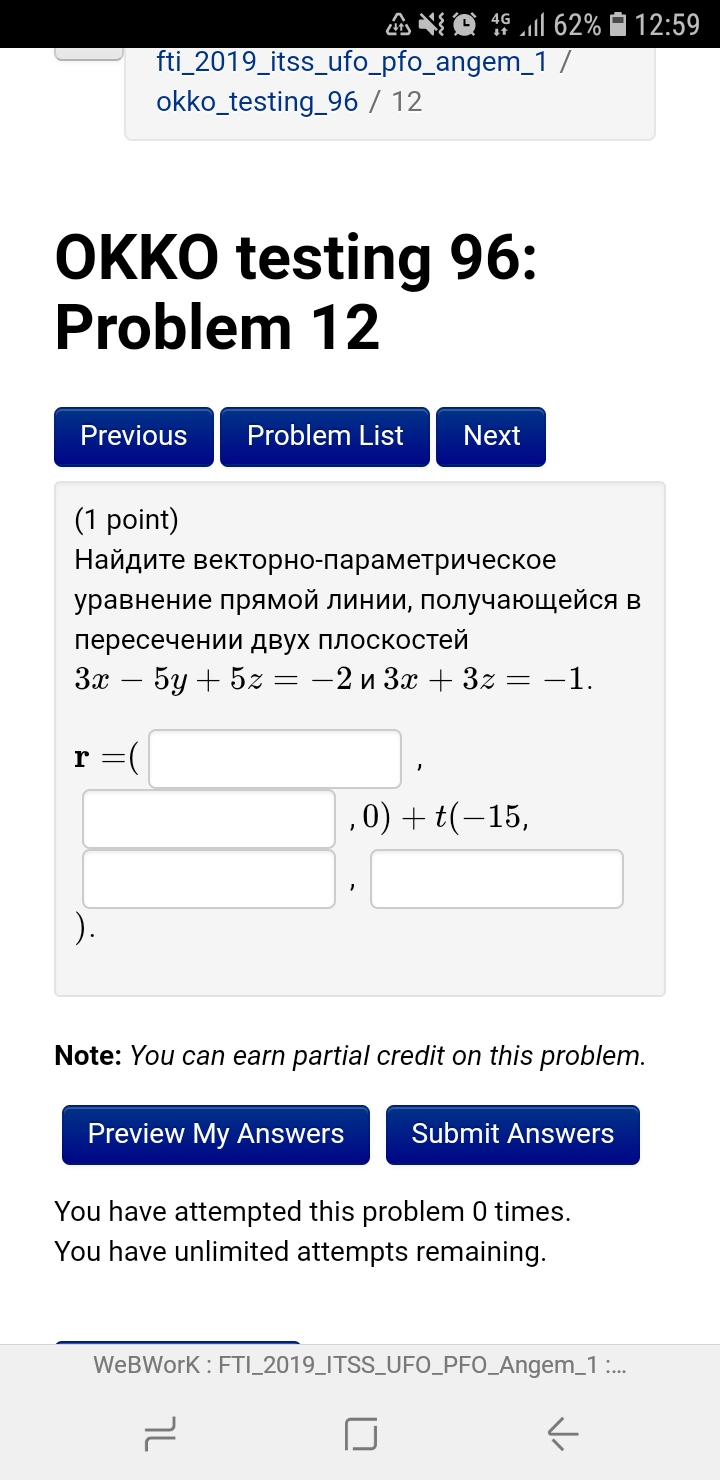
Векторно–параметрическое уравнение:
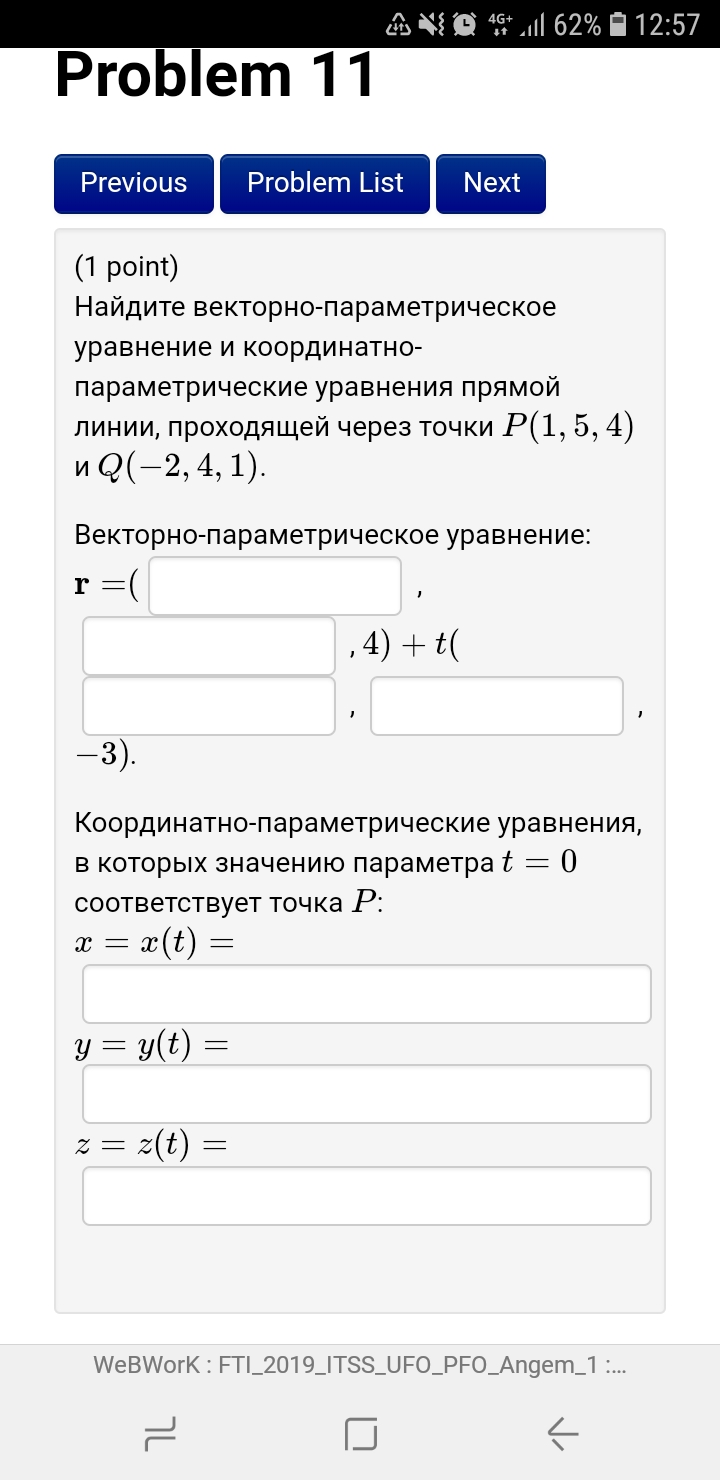
r = ( , , 4) + t ( , , –3).

Координатно–параметрические уравнения, в которых значению параметра t = 0 соответствует точка P:
x = x(t) =

y = y(t) =

z = z(t) =

Найдите векторно–параметрическое уравнение и координатно–параметрические уравнения прямой линии, проходящей через точку P(0, –5, 4) и перпендикулярной плоскости –3x + 3y + 2z = 3.

Составить уравнение плоскости, которая проходит через точку M1(–2,5;–6) параллельно плоскости 2x–3y+5z–7=0

Исследовать взаимное расположение плоскостей x–3y+5=0 и 2x–y+5z–16=0 . В случае их параллельности найти расстояние между ними, в случае пересечения – угол между ними.

Векторы a={1;0;1} и b={0;1;1} является сторонами треугольника. Найти высоту этого треугольника .

Найдите острый угол между прямой (x=t–1 y=–t+2 z= √2t) и плоскостью x+y+ √2z+5=0

Две стороны квадрата лежат на прямых 3x–4y–4=0 и 3x–4y+11=0 . Чему равна площадь квадрата?

Найти точку пересечения прямой, проходящей через точки M1(–2;2;1), M2(0;2;–1) и плоскости x+2y–2z+6=0 .

Найти m и n, если плоскости 2x+3y+nz–1=0 и mx+6y–2z=1 параллельны.

x+y–1=0 2x+3y+4=0 провести прямую перпендикулярно к прямой 3x–y+7=0

помогите решить пожалуйста срочно номер №3 №4 №5

Будьте добры решить что сможете несколько задач, лёгкие, просто нужны формулы.
1)Вычислить высоту BD треугольника заданного своими вершинами
A(1; − 2; 8); B(0; 0; 4); C(6; 2; 0)
Ответы: а) 0,5; б) 3; в) –1,5; с) 1,5
2)Даны векторы a = (2;1; 4); G b = (3; 0; 3); G c = (3;1; 0). G
Вычислить: a × c + 2 b × c + a × b
Ответы: а) не имеет смысла; б) 18 + 161 + 99;
в) (−3; 9; 3); г) 18 + 260;
Указание: Исходить из определения векторного произведения и модуля век–
тора.
3) При каких α и β векторы a и b коллинеарны, если
a = αi + 5 j − k , b = 3i + j + βk
Ответы: а) 15 и 1; б)–15 и 1; в)15 и ;
5
1 − г)
5
1
и –15;
4) Даны векторы a = (1; − 3; 4); G b = (3; − 4; 2); c = (−1;1; 4).
Найти: npb+ca .
Ответы: а) –5; б) 8; в) 5; г)–8;
5) Показать, что точки A(5; 7; − 2); B(3; 1; −1); C(9; 4; − 4); D(1; 5; 0);
лежат в данной плоскости.Указание: Показать, что (AB, AC, AD) = 0
4 1 4 1 4 1
3 1 3 1 3 1
2 1 2 1 2 1
=
− − −
− − −
− − −
x x y y z z
x x y y z z
x x y y z z
Ответы: а)12; б) 48; в)–12; г)0
И последнее
Какую кривую второго порядка определяет каждое из заданных уравнений?
Найти все известные вам их характеристики.
а) у
2
–8х+12у+76=0; б) 1
1
−
− + = x
x
y .

Даны вектора а(3:0:4) b (7:0:2) запишите координаты вектора с если
1) с=a+b
2) c=2a+b

5. Найти параметрическое уравнение прямой.

записать уравнение и определить вид поверхности, полученной при вращении данной линии вокруг указанной оси координат, сделать рисунок
1) 15x² – 3y² = 1, Ox
2) x=3, y=4, Oz

Записать уравнение и определить вид поверхности, полученной при вращении данной линий вокруг указанной оси координат, сделать рисунок
5x²–6z²=30, OX

Найти координаты точки пересечения плоскости, про– ходящей через точки А = (−2;1;−2), В = (2;−1;−4), С = (−8;5;1) с прямой, проходящей через точки D = (30;−19;−21), Е = (6;−3;−5).


Найти координаты точки, симметричной точке А = (4,2,−8) относительно плоскости, заданной уравнением −2·х+1·у−3·z−4=0.


Найти координаты проекции точки A = (4,−5,3) на прямую, проходящую через точки В = (−1,−3,3) и С = (−5,0,4).

III уровень, 2 вариант

Найти площадь треугольника АВС с вершинами А(–2,0,1) , В(2,3,2), С(2,5,3)

Найти проекцию точки М(1,4,3) на плоскость 3x – y + 2z + 9 = 0.

Введите координаты x0, y0, z0 проекции точки в указанном порядке.

В прямоугольном пароллелепипеде ABCDA1B1C1D1
AB=AA1=2,BC=3,точка М– середина АВ
Найти :
а) длину отрезка МD1
б) угол между А1М и AD1
в) расстояние от точки D до плоскости В1СМ
г) угол между DM и плоскостью В1СМ
д) угол между плоскостями В1СМ и АСD1

Найти объем пирамиды ABCD с вершинами: А(5,2,–2), В(2,–2,–1), С(3,1,4), D(1,2,2).

Написать уравнение плоскости , проходящей через точки Р(3,–1,–2) и Q(7,–3,4) и пенпендикулярной к заданной плоскости x+4y–2z–3=0

Найдите точку пересечения прямой и плоскости, заданных уравнениями

(x – 1) / 1 = (y / 0) = (z + 3) / 2 , 2x – y + 4z = 0.

Запишите каноническое уравнение прямой, проходящей через точку M(1;–4;5) параллельно вектору ā={0;–2;1}
помогите с этим примером очень нужно, заранее Спасибо!

Даны две точки A(–2;4) ,B (3;–2)
Найти положение точки C при котором площадь ABC = 70

решите пожалуйста 5 задачу

Известна точка пересечения диагоналей квадрата K(1,5; 2,5) и уравнение одной из его сторон х–4у=0 . Найти координаты вершин квадрата и составить уравнения его диагоналей

Составить уравнение прямой проходящей через точку М (–1,1,1)и точку пересечения прямой (x+8)/1=(y–5)/(–2)=z/3 и плоскости x+y+x+1=0

Найти точку A, симметричную точке B(–2, 1) относительно прямой 3x+2y–1=0

10. Найдите точку пересечения прямой и плоскости, заданных уравнениями

[m] \frac{x-1}{-1} = \frac{y+5}{4} = \frac{z-1}{2} , \, x-3y+7z-24=0. [/m]

11. Найдите точку [m] M' [/m] симметричную точке [m] M [/m] относительно прямой, если: [m] M(2,-1,1) [/m],

[m] \frac{x-4,5}{1} = \frac{y+3}{-0,5} = \frac{z-2}{1} [/m]

··Вариант 4··

1. Найдите угол между прямыми на плоскости у=37+х и у=19–х.

2. Найдите уравнение прямой, проходящей через точку М(2;4) перпендикулярно к прямой у=6х–7.

3. Найдите уравнение прямой, проходящей через две данные точки А(–8, 0) и В(–3, 2).

4. Найдите площадь квадрата, стороны которого лежат на
прямых 3х–4у+10=0 и 6х–8у–13=0.

5. Составьте уравнение плоскости, проходящей через точку А перпендикулярно вектору [m]\mathbf{n}[/m], если А(– 10,0,9), В(12,4,11), С(8,5,15).

6. Известно, что одна из граней куба находится на плоскости, проходящей через три точки А (1,1, –7), В( 1, 2, –4) и С (–3, –2, 0), а одна из вершин – точка Д(–1, 7, –1).
а) найдите объем куба;
б) найдите уравнение ребра куба, проходящего через точку Д перпендикулярного грани, лежащей на плоскости АВС;
в) уравнение плоскости, на которой лежат грань куба, параллельная плоскости АВС, и точка Д.

7. Найдите угол между плоскостями
[m] 3x+У+2z+15=0 [/m]
и
[m]5х+9у-3z=0.[/m]

8. Найдите координаты точки А, равноудаленной от точек В и С, если: А(0.0.z), B(–1,1,–6), С (2.3.5)

9. Составте канонические уравнения прямой, заданной пересечением плоскостей x+y+2=0 и x+y–2z+2=0.

Задача 1–Т15–3 Высшая Математика для 1–го курса

Задача 1–Т15–6 Высшая Математика для 1–го курса

1–Т15–8 Прислать в электронном листе как на фото, или фото решение записанной на бумаге

1–Т15–7 Прислать в электронном листе как на фото, или фото решение записанной на бумаге

1–Т15–6 Прислать в электронном листе как на фото, или фото решение записанной на бумаге

1–Т15–5 Прислать в электронном листе как на фото, или фото решение записанной на бумаге

1–Т15–4 Прислать в электронном листе как на фото, или фото решение записанной на бумаге

1–Т15–3 Прислать в электронном листе как на фото, или фото решение записанной на бумаге

Задача 1–Т15–7 Высшая Математика для 1–го курса

1–Т15–2 Прислать в электронном листе как на фото, или фото решение записанной на бумаге

1–Т15–1 Прислать в электронном листе как на фото, или фото решение записанной на бумаге

Помогите решить задание 1,2,3,4,5

составить каноническое и параметрическое уравнение прямой
{2x+y–z=0
{3x–y–z–2=0

найти проекцию точки (0;–1;–4) на прямую
{2x+y–z=0
{3x–y–z–2=0

составить уравнение прямой
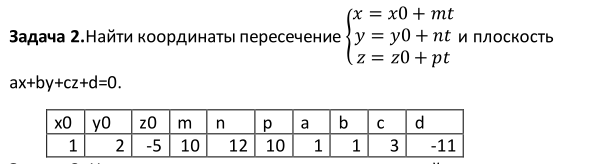
{2x+y–z=0
{3x–y–z–2=0
проходящей через точку (0;–1;–7) параллельно вектору (1;–1;0). Доказать, что прямая
{2x+y–z=0
{3x–y–z–2=0 параллельна плоскости 2x–y+z–3=0 и найти расстояние между
{2x+y–z=0
{3x–y–z–2=0 и 2x–y+z–3=0

Найдите длину отрезка, отсекаемого от оси аппликат плоскостью, про– ходящей через точки P 1 (2,1,0), P 2 (1,0,4) и пересекающей оси ординат и абсцисс в точках A 1 (0,a,0), A 2 (a,0,0)

Даны три последовательные вершины параллелограмма А(1;3) В(0;2) С(–1;–2). Не находя координатов вершины D, найти: уравнение стороны АD

4 задания под в

Даны координаты вершин пирамиды. Найти: 1) длины ребер АВ и AC; 2) угол
между ребрами АВ и АС; 3) площадь грани АВС; 4) объем пирамиды ABCD; 5)
уравнение прямой АВ; 6) уравнение плоскости АВС; 7) уравнение высоты
пирамиды, опущенной на грань АВС. Сделать чертеж.

Запишите общее уравнение плоскости, в котором коэффициент при переменной x равен –8. если известно, что плоскость проходит через три (0,4,–1), (3,1,1),(3,2,3).

Дана прямая x+y–2z–1=0
x–y–z+2=0
Найти ее


канонические уравнения.

Даны вершины треугольника ABC. Найти: а) уравнение стороны AB; б) уравнение высоты CH; в) уравнение медианы AM; г) точку персечения медианы AM и высоты CH; д) уравнение прямой, проходящей через вершину C параллельно стороне AB; е) расстояние от точки C до прямой AB
A(–3,8); B(–6;2); C(0,–5)

Создатель