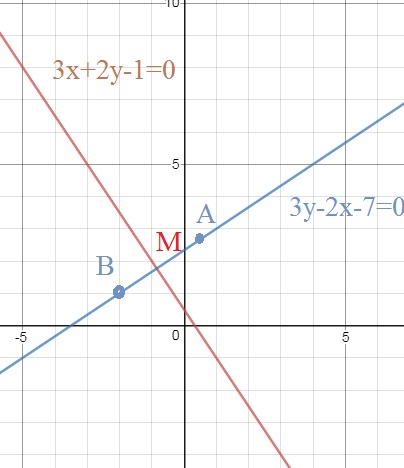Задача 32579 Найти точку A, симметричную точке B(-2,...

jakson

2019-01-07 21:43:51

Найти точку A, симметричную точке B(-2, 1) относительно прямой 3x+2y-1=0

sova

2019-01-07 22:05:27

★

Составляем уравнение прямой, перпендикулярной данной прямой и проходящей через точку B

3х+2у-1=0 ⇒ у=-(3/2)х+(1/2)
угловой коэффициент k=(-3/2)
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
k=2/3 - угловой коэффициент искомой прямой
y=(2/3)x+b - множество прямых, перпендикулярных данной.
чтобы выделить прямую, проходящую через точку B
подставим координаты точки В

1=(2/3)*(-2)+b
b=7/3

y=(2/3)x+(7/3)

Найдем координаты точки М - точки пересечения двух прямых
{3x+2y-1=0
{y=(2/3)x+(7/3)

3x+2*((2/3)x+(7/3))-1=0
(13/3)x+(11/3)=0
x=(-11/13)
y=69/39=23/13

По свойству симметричных точек
ВМ=МА
x_(M)=(x_(B)+x_(A))/2 ⇒
x_(A)=2x_(M)-x_(B)=(-22/13)-(-2)=4/13

y_(M)=(y_(B)+y_(A))/2 ⇒ y_(A)=2y_(M)-y_(B)=2*(23/13)-1=33/13

О т в е т. (4/13; 33/13)