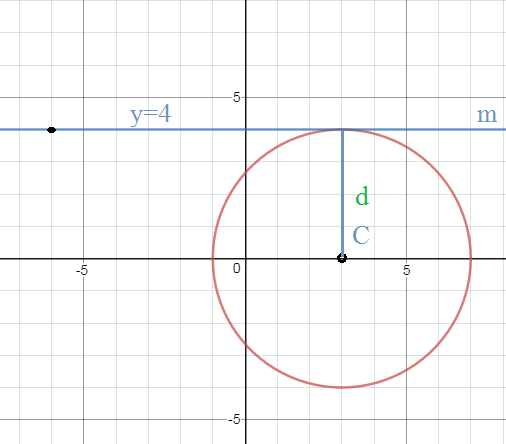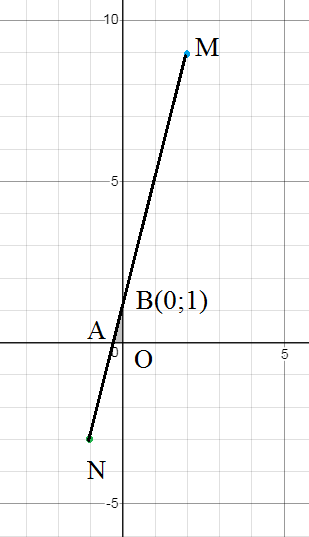Задача 32148 III уровень, 2 вариант...

vk406384213

2018-12-19 19:30:31

III уровень, 2 вариант

sova

2018-12-19 20:21:28

★

1.x^2-10x+4x+y^2=7
Выделяем полный квадрат
(x^2-6x)+y^2=7
(x^2-2*3x+3^2) - 3^2 +y^2=7
(x-3)^2+y^2=16

Уравнение окружности вида (x-a)^2+(y-b)^2=R^2

a=3; b=0
R=4

Центр окружности C(3;0)
Прямая, проходящая через точку (-6;4), параллельно оси абсцисс
y=4

d(C;m)=4

2.
Cоставим уравнение прямой MN
y=kx+b
Подставляем координаты точек M и N
{9=k*2+b
{-3=k*(-1)+b

Вычитаем
12=3k
k=4


b=9-2k=9-2*4=1

y=4x+1

Прямая MN пересекает оси координат в точках:
x=0; y=1
B(0;1)
y=0;
4x+1=0
x=-1/4
A(-1/4;0)

Треугольник АОВ - прямоугольный.
S=(1/2)AO*OB=(1/2)*(1/4)*1=1/8

О т в е т. S=1/8

3.
{x-y=4
{x^2+y^2=16

{у=х - 4
{x^2+y^2=16

x^2+(x-4)^2=16

x^2+x^2-8x+16=16
2x^2-8x=0
2x*(x-4)=0
x=0 или x=4
y=4 или у=0

Прямая х - у = 4 пересекает окружность в двух точках
(0;4) и (4;0)

d=sqrt(2^2+2^2)=2sqrt(2)