Задача 41259 Найти уравнение сторон треугольника,...
Условие
Все решения
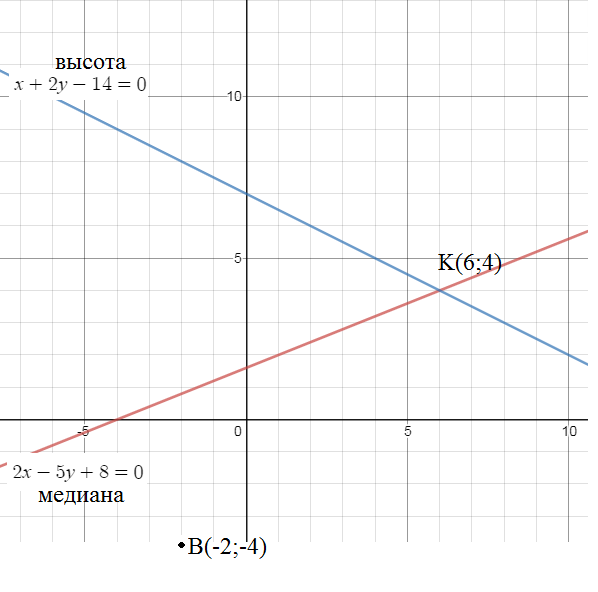
{2x-5y+8=0
{x+2y-14=0
Умножаем второе уравнение на 2
{2x-5y+8=0
{2x+4y-28=0
Вычитаем из первого второе
{-9y+36=0 ⇒ y=4
{x+2y-14=0 ⇒ x=14-2y=14-2*4=6
точка имеет координаты (6;4)
Назовем ее точка К
Скорее всего дана точка В и два уравнения медианы и высоты,
проведенных из других вершин треугольника
Составим уравнение прямой ВК, как прямой проходящей через две точки:
[m]\frac{x-x_{В}}{x_{К}-x_{В}}=\frac{y-y_{В}}{y_{К}-y_{В}}[/m]
[m]\frac{x-(-2)}{6-(-2)}=\frac{y-(-4)}{4-(-4)}[/m]
[m]\frac{x+2)}{8}=\frac{y+4)}{8}[/m]
х+2=y+4
[b]x-y-2=0 [/b]- уравнение ВК
высота x+2y-14=0 и ВК не перпендикулярны,так как произведение угловых коэффициентов взаимно перпендикулярных прямых должно быть равно (-1).
Значит высота перпендикулярна стороне ВМ.
Координату точки М требуется найти
Уравнение стороны ВМ, как прямой, перпендикулярной x+2y-14=0
и проходящей через точку В легко написать.
x+2y-14=0 ⇒ y=-[m]\frac{1}{2}x+7[/m]
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
Значит, угловой коэффициент стороны ВМ
k_(BM)=2
Общий вид такой прямой
y=2x+b
Так как ВМ проходит через точку В, подставим ее координаты в уравнение
y=2x+b
и найдем b
-4=2*(-2)+b
b=0
уравнение BM: [b]y=2x[/b]
Найдем координаты точки пересечения ВМ и медианы.
Решаем систему уравнений:
{2х–5у+8=0
{y=2x
2x-5*(2x)+8=0
-8x+8=0
x=1
y=2
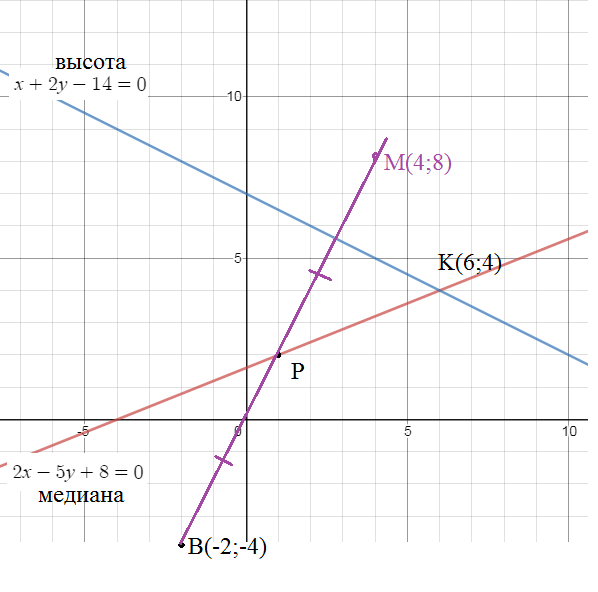
Пусть это точка Р(1;2)
Точка Р - середина ВМ
x_(P)=[m]\frac{x_{B}+x_{M}}{2}[/m]
y_(P)=[m]\frac{y_{B}+y_{M}}{2}[/m]
x_(M)=2x_(P)-x_(B)=2*1-(-2)=4
y_(M)=2y_(P)-y_(B)=2*2-(-4)=8
M(4;8)
Уравнение КМ, как уравнение прямой проходящей через две точки:
[m]\frac{x-x_{K}}{x_{M}-x_{K}}=\frac{y-y_{K}}{y_{M}-y_{K}}[/m]
[m]\frac{x-6}{4-6}=\frac{y-4}{8-4}[/m]
[b]2х+у-8=0[/b] - уравнение МК
О т в е т. x-y-2=0; y=2x; 2х+у-8=0