Задача 43452 1. Составить уравнение прямой, если...

vk557167629

2020-01-16 23:38:52

1. Составить уравнение прямой, если известно, что точка Р (2;3) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.

2. Даны два вектора: а= (3;–1;5), b= (1;2;–3) . Найти вектор при условии, что он перпендикулярен к оси OZ и удовлетворяет условиям: xa=9, xb=4.
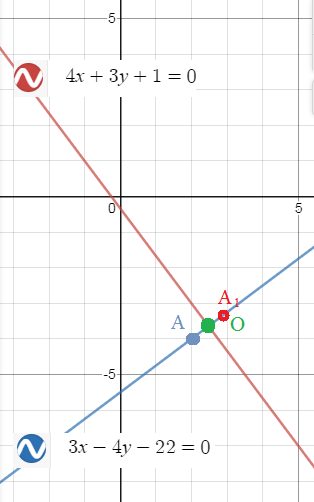
3. Найти координаты точки, симметричной точке (2;–4), относительно прямой 4x+3y+1=0.

sova

2020-01-16 23:45:46

1.
Составим уравнение перпендикуляра, который проходит через начало координат и точку Р

y=(3/2)x

Угловые коэффициенты перпендикулярных прямых в произведении дают -1

Значит угловой коэффициент прямой (-2/3)

y=(-2/3)x+b

Чтобы найти b подставим координаты точки Р и получим ответ

2.
vector{x}=(m;k;n)

xa=9
[b]3m-k+5n=9[/b]

xb=4
[b]m+2k-3n=4[/b]

vector{x} перпендикулярен к оси OZ ⇒
x*i=0
[b]m*1=0[/b]

Решаем систему трех уравнений
находим координаты вектора х



3. Составляем уравнение прямой, перпендикулярной

4x+3y+1=0 и проходящей через точку (2;-4)

4x+3y+1=0 ⇒ y=-(4/3)x -(1/3)
k= -4/3

перпендикулярная прямая

y=(3/4)x+b

Подставляем координаты точки A(2;-4) и находим b

b=-11/2

y=(3/4)x-(11/2)

Находим координаты точки O- точки пересечения прямых
{4x+3y+1=0
{y=(3/4)x-(11/2)

4x+3*((3/4)x-(11/2))+1=0


Координаты точки А_(1), симметричной точке А находим из условия, что О-середина АА_(1)

точка