ВЕКТОРЫ
Подкатегории (2)
Практика (83)



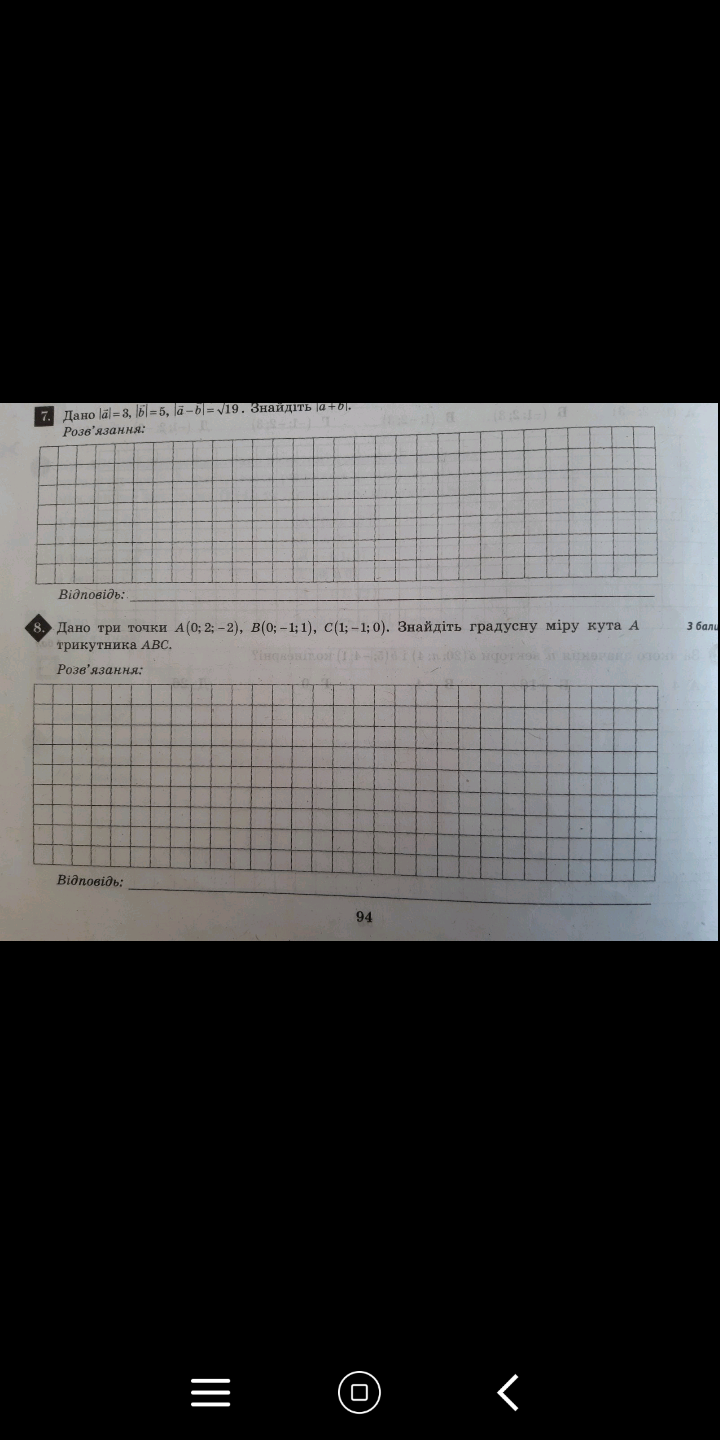
Найти площадь параллелограмма построенного на векторах и длину вектора а.
На втором фото пример решения. Еще должна быть проверка вроде как


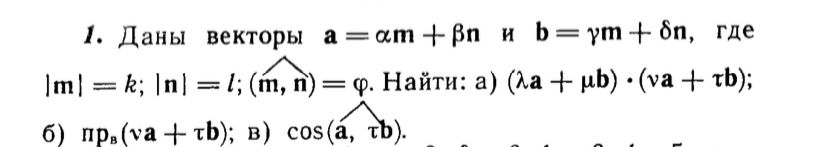
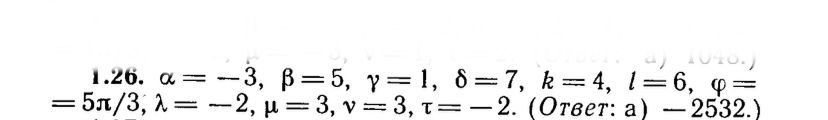

г) скалярное произведение векторов \( (MA + MC) \cdot MB = \)

2)даны векторы
3)известно что
4)найти проекцию вектора
На рёбрах B1C1 и C1D1 соответственно отмечены точки N и M так, что B1N:NC1=1:4;C1M:MD1=1:4.
Определи косинус угла α между прямыми BN и CM, если ребро куба равняется 1 ед. изм.
Ответ: cosα=
F = (-9,5,7), A(1,6,-3), B(4,-3,5)
Площадь параллелограмма, построенного на векторах a, b, равна S = 3. Найти высоту
параллелепипеда, построенного на векторах 2a + b, a − b, a + b + 4c, которая опущена из
конца третьего вектора на грань, построенную на первых двух.
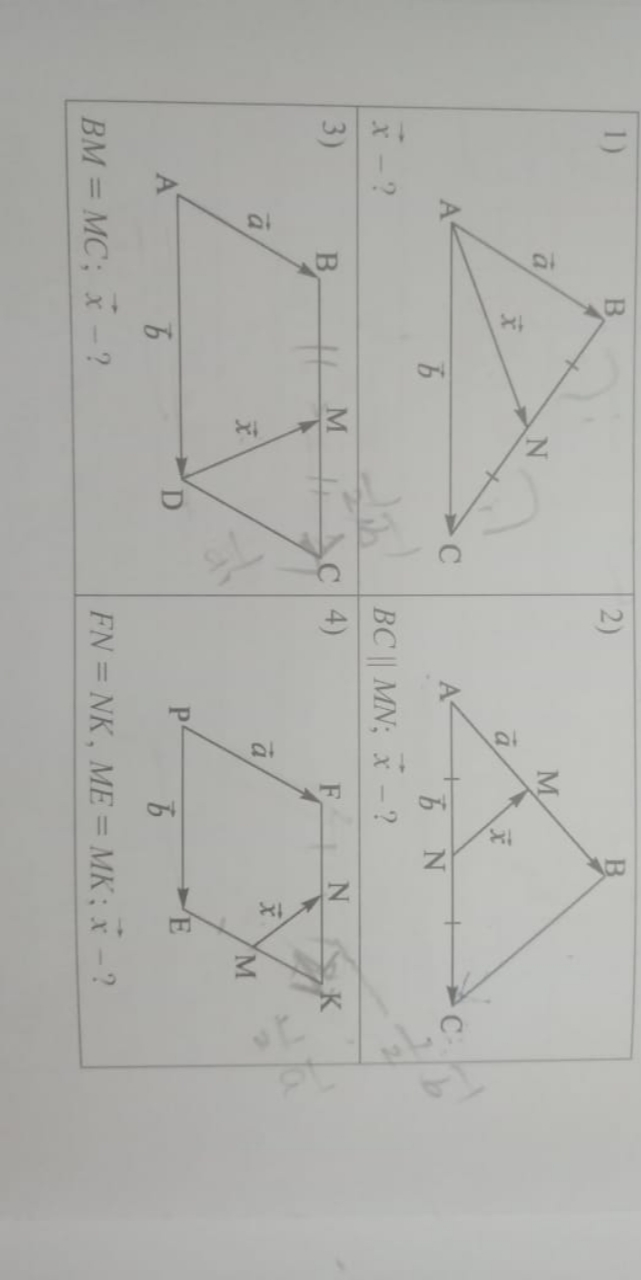
2)AB-DA+CD-OD=?


Постройте эту призму и координатным методом найдите:
а) величину угла между прямыми АВ1 и СF1;
б) синус угла между прямой В1E и плоскостью ВС1С;
в) косинус угла между (АВС) и (ВС1F).
□ **α**=--6 и **β**= 2/3
□ **α**=--2/3 и **β**=6
□ **α**=2/3 и **β**=--6
□ **α**=6 и **β**=--2/3


[m]\vec{a} = 2i + j - 3k[/m]
[m]\vec{b} = -j + k[/m]
A) 8; B) [m]2\sqrt {3}[/m]; C) [m]\sqrt {3}[/m]; D)4; E) 2
6. Найти объём треугольной пирамиды, образованной векторами:
[m]\vec{a} = -7i + 2j - 2k[/m],
[m]\vec{b} = -2i + 4j - 7k[/m]
[m]\vec{c} = -3i - 2j + k[/m]
A) 84; B) 14; C)7; D)8; E) 2

Представить вектор [m]\mathbf{d} = (4; 12; -3)[/m] как линейную комбинацию
векторов [m]\mathbf{a} = (2; 3; 1)[/m], [m]\mathbf{b} = (5; 7; 0)[/m] и [m]\mathbf{c} = (3; -2; 4)[/m].
a) косинус угла между векторами m ⃗ и n ⃗;
b) число х, если векторы m ⃗ и a ⃗ коллинеарны;
с) число x , если векторы n ⃗ и a ⃗ перпендикулярны.
[m]\overrightarrow{OA} = \vec{r}, \ \vec{F} = 7p - 2q, \ \vec{r} = p + 3q, \ |\vec{p}| = \frac{1}{2}, \ |\vec{q}| = 2, \ (\vec{p}, \vec{q}) = \frac{\pi}{2}[/m].
Заранее спасибо)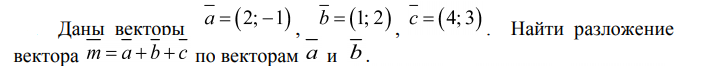

Показать, что... образует базис в множестве всех векторов на плоскости.
Построить заданные векторы и найти разложение вектора .. по векторам

№16.Вычислите работу A, которую совершает сила F → (–3; 4), когда ее точка приложения, двигалась прямолинейно, перемещается из положения B(5; –1) в положение C(2; 1).
№14. Найдите скалярное произведение векторов AB → и BC → , если A(0; –5), B(3; 6), C(–8; 10);
A)44; B)33; C)22; D)11.


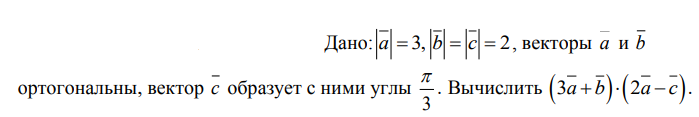

Нужно подробное объяснение (для понимания) 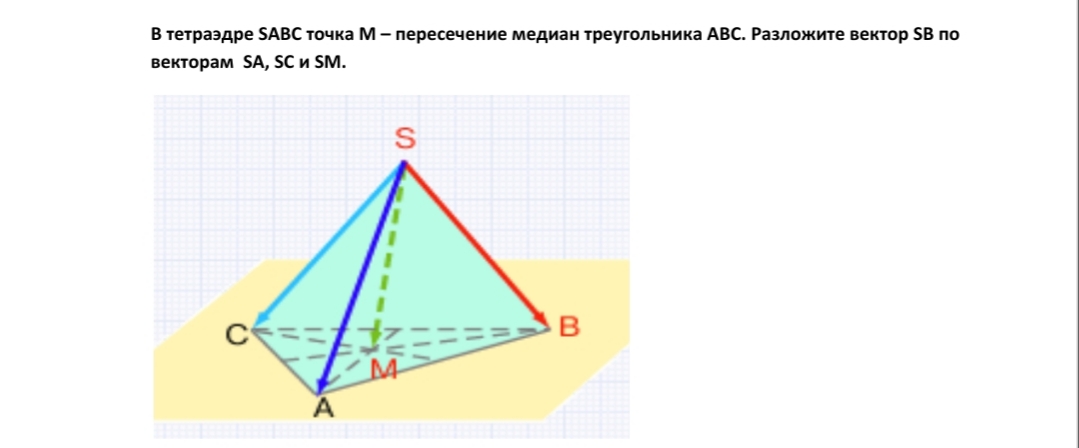
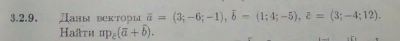
Найти угол между векторами [m]\overline{AB}[/m] и [m]\overline{AC}[/m].
Даны векторы a = –3m + 4n и b = 5m –7n, где |m| =2, |n| = 6,∠(m,n) =4π/3.
Найти:
а) (3а –2b)( 3а + 4b),
б) Пр_в(3а + 4b),
d) cos ∠ (a, b)
АВ = m, АД =n и AA1 = p . Построить следующие векторы: -m + n -p и 2м-n+1\2p
1) длину вектора a+b
2) координаты векторам m если известно, что длина вектора m втрое больше длины вектора а
2.Даны вектора:a (3:0:4) b (7:0;2).Найдите.1) при каком значении k вектор n (k;0;6) коллинеарные вектору b;
2) или компланарные вектора a,b и j (0;0;1)


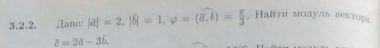
|а|=3,|b|=4, угол (а, b) =120°
|а+в|=3, |а-в|=1

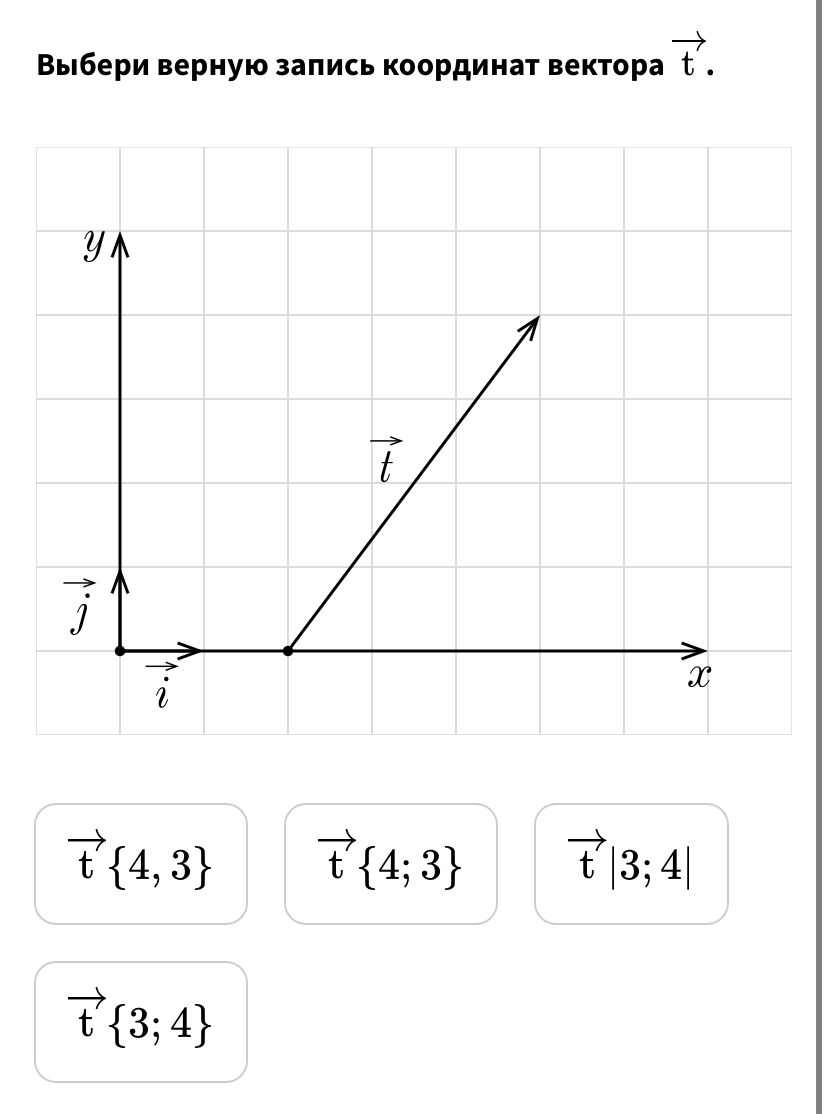
Вычисли координаты конечной точки вектора, который получится из данного вектора параллельным переносом на вектор m→(0;3).
Координаты конечной точки: (
;
).
Дополнительный вопрос:
изменятся ли координаты полученного вектора?
1) Нет
2) Невозможно определить
3) Да
вектор AB (2; -1; 4) и точки C (3; 0; -2) и D (1; -1; 2)
Найти:
а) координаты вектора DC;
б) абсолютную величину вектора AB;
в) координаты вектора AB - DC
9 клас КР № 2 Вектори на площині Варіант ІІ
Дано вектори c ⃗(-2;7) і d ⃗(6;5). Укажіть координати вектора m ⃗, якщо m ⃗=c ⃗+d ⃗.
А. (-8;2). Б. (4;2) В. (4;12). Г. (-8;12).
Дано вектори a ⃗(5;-9) і b ⃗(2;1). Укажіть координати вектора n ⃗, якщо n ⃗=a ⃗-b ⃗.
А. (7;-8). Б. (-3;-10) В. (3;10). Г. (3;-10).
Знайдіть скалярний добуток векторів p ⃗(-3;4) і n ⃗(2;5).
А. 14. Б. 0 В. 26. Г. -26.
Знайдіть координати вектора (AB) ⃗ та модуль, якщо A(-2;3), B(3;15). , завдання за 20.03, виконати свій варіант в зошиті
Дано вектори a ⃗(9;-6) і b ⃗(2;3). Знайдіть координати вектора l ⃗=1/3 a ⃗-2b ⃗.
Дано вектори m ⃗ і n ⃗. Побудуйте вектори:
d ⃗=m ⃗+n ⃗;
c ⃗=m ⃗-n ⃗.
Дано вектори a ⃗(-2;y) і b ⃗(4;10). При якому значенні y вектори a ⃗ і b ⃗:
колінеарні;
перпендикулярні.
Знайдіть кут між векторами c ⃗(-3;0) і d ⃗(-1;1).
Доведіть за допомогою векторів, що чотирикутник з вершинами в точках M(6;2), N(8;8), K(6;14) і L(4;8) – ромб.
Найди значение [m]x[/m], если [m]\vec{a} \cdot \vec{b} = 29[/m].
Найди значение [m]x[/m], если [m]\vec{a} \cdot \vec{b} = 4[/m].
2. Даны два вектора: а= (3;–1;5), b= (1;2;–3) . Найти вектор при условии, что он перпендикулярен к оси OZ и удовлетворяет условиям: xa=9, xb=4.
3. Найти координаты точки, симметричной точке (2;–4), относительно прямой 4x+3y+1=0.
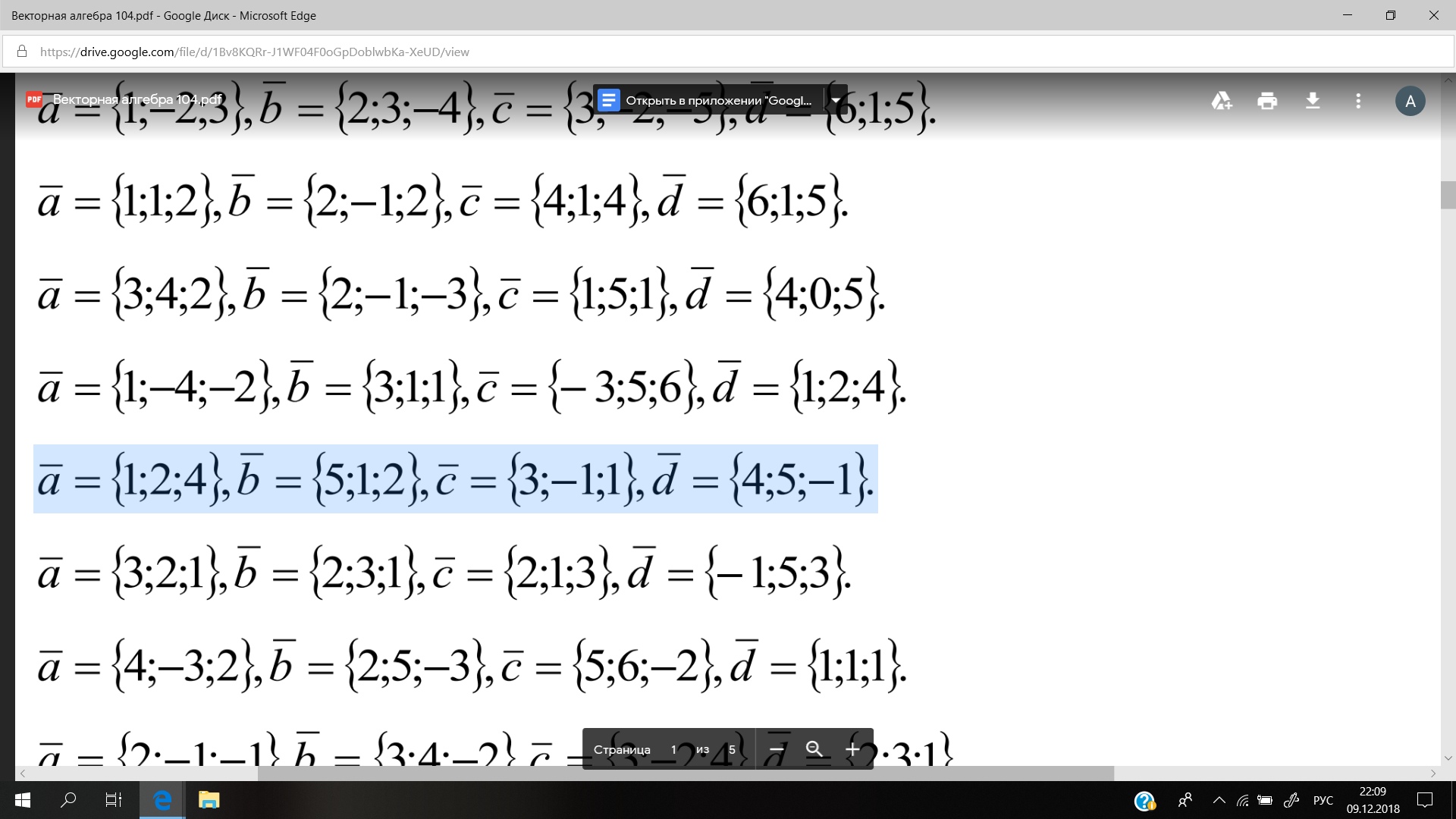

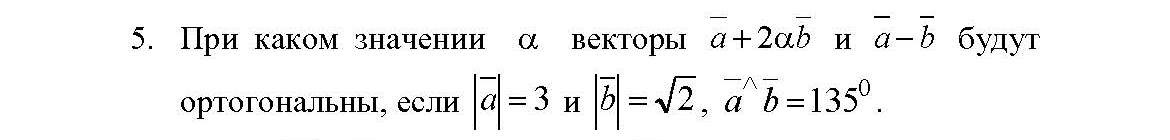
координаты вектора d в этом базисе.
a =(- 2, 1, 7) , b =(3, - 3, 8) , c =(5, 4, - 1) , d =(18, 25, 1) 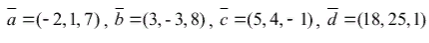


Редакторы (1)
 SOVA
SOVA
Создатель