Задача 55297 Помогите с данным заданием. Как всегда...
Условие
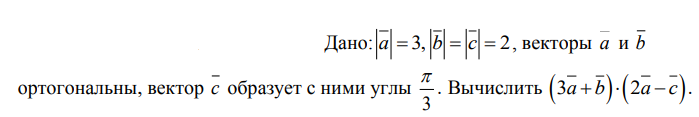
Решение
Находим скалярное произведение:
[m](3\vec{a}+\vec{b})\cdot (2\vec{a}-\vec{c})= [/m]
векторная АЛГЕБРА, поэтому как в алгебре раскрываем скобки:
[m]=3\vec{a}\cdot 2\vec{a}+\vec{b}\cdot 2\vec{a}+3\vec{a}\cdot(-\vec{c})+\vec{b}\cdot (-\vec{c})=6\cdot ( \vec{a})^2+2\cdot \vec{a}\cdot \vec{b}-3\cdot \vec{a}\cdot\vec{c}-\vec{b}\cdot \vec{c}=6\cdot 9 +0-3\cdot 3-2=43[/m]
так как
скалярный квадрат:
[m]( \vec{a})^2=|\vec{a}|\cdot |\vec{a}|\cdot cos 0^{o}=( |\vec{a}|)^2=3^2=9[/m] ;
скалярное произведение [m] \vec{a}\cdot \vec{b}=|\vec{a}|\cdot |\vec{b}|\cdot cos∠ ( \vec{a},\vec{b})=0[/m]
так как [m] ∠ ( \vec{a},\vec{b})=90^{o}[/m] и [m]cos 90^{o}=0[/m]
скалярное произведение [m] \vec{a}\cdot \vec{c}=|\vec{a}|\cdot |\vec{c}|\cdot cos∠ ( \vec{a},\vec{c})=3\cdot 2\cdot cos \frac{π}{3}=3\cdot 2\cdot \frac{1}{2}=3[/m]
скалярное произведение [m] \vec{b}\cdot \vec{c}=|\vec{b}|\cdot |\vec{c}|\cdot cos∠ ( \vec{b},\vec{c})=2\cdot 2\cdot cos \frac{π}{3}=2\cdot 2\cdot \frac{1}{2}=2[/m]
Ответ: 43