Задача 67385 #Рябушко. -> ->...
Условие
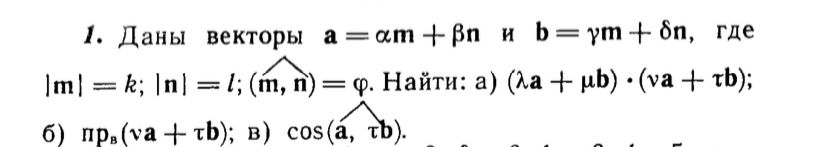
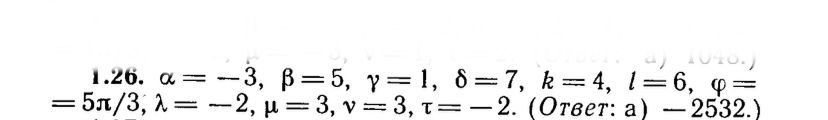
Решение
[m]\vec{b}=\vec{m}+7\vec{n}[/m]
a)[m](-2\vec{a}+3\vec{b})\cdot (3\vec{a}-2\vec{b})=[/m] раскрываем скобки как в алгебре ( векторная алгебра)
[m]=-6\vec{a}\cdot \vec{a}+9 \vec{b}\cdot \vec{a}+4\vec{a}\cdot \vec{b}-6\vec{b}\cdot \vec{b}=-6\vec{a}\cdot \vec{a}+13 \vec{a}\cdot \vec{b}-6\vec{b}\cdot \vec{b}=[/m]
так как по свойствам скалярного произведения [m]\vec{b}\cdot \vec{a}=\vec{a}\cdot \vec{b}[/m]
Находим:
[m]\vec{a}\cdot \vec{a}=(-3\vec{m}+5\vec{n})(-3\vec{m}+5\vec{n})=9\vec{m}\cdot \vec{m}-30\vec{m}\cdot \vec{n}+25\vec{n}\cdot \vec{n}[/m]
[m]\vec{a}\cdot \vec{b}=(-3\vec{m}+5\vec{n})(\vec{m}+7\vec{n})=-3\vec{m}\cdot \vec{m}-16\vec{m}\cdot \vec{n}+35\vec{n}\cdot \vec{n}[/m]
[m]\vec{b}\cdot \vec{b}=(\vec{m}+7\vec{n})(\vec{m}+7\vec{n})=\vec{m}\cdot \vec{m}+14\vec{m}\cdot \vec{n}+49\vec{n}\cdot \vec{n}[/m]
По определению скалярного произведения:
[m]\vec{m}\cdot \vec{n}=|\vec{m}|\cdot| \vec{n}|\cdot cos\frac{5π}{3}=4\cdot 6\cdot \frac{1}{2}=12[/m]
[m]\vec{m}\cdot \vec{m}=|\vec{m}|\cdot| \vec{m}|\cdot cos0=4\cdot 4\cdot 1=16[/m]
[m]\vec{n}\cdot \vec{n}=|\vec{n}|\cdot| \vec{n}|\cdot cos0=6\cdot 6\cdot 1=36[/m]
Тогда
[m]\vec{a}\cdot \vec{a}=9\vec{m}\cdot \vec{m}-30\vec{m}\cdot \vec{n}+25\vec{n}\cdot \vec{n}=9\cdot 16-30\cdot 12+25\cdot 36=144-360+900=684[/m]
[m]\vec{a}\cdot \vec{b}=-3\vec{m}\cdot \vec{m}-16\vec{m}\cdot \vec{n}+35\vec{n}\cdot \vec{n}=-3\cdot 16-16\cdot 12+35\cdot 36=1020[/m]
[m]\vec{b}\cdot \vec{b}=\vec{m}\cdot \vec{m}+14\vec{m}\cdot \vec{n}+49\vec{n}\cdot \vec{n}=16+14\cdot 12+49\cdot 36=1948[/m]
Таким образом
[m](-2\vec{a}+3\vec{b})\cdot (3\vec{a}-2\vec{b})=-6\vec{a}\cdot \vec{a}+13 \vec{a}\cdot \vec{b}-6\vec{b}\cdot \vec{b}=-6\cdot 684+13\cdot 1020-6\cdot 1948=-2532[/m]
б)
пр[m]_{\vec{b}}(3\vec{a}-2\vec{b})=\frac{(3\vec{a}-2\vec{b})\cdot \vec{b}}{|\vec{b}|}[/m]
[m]|\vec{b}|^2=\vec{b}\cdot \vec{b}=1948[/m]
[m](3\vec{a}-2\vec{b})\cdot \vec{b}=3\vec{a}\cdot \vec{b}-2\vec{b}\cdot \vec{b}=3\cdot1020-2\cdot 1948=3060-3896=-836[/m]
пр[m]_{\vec{b}}(3\vec{a}-2\vec{b})=\frac{(3\vec{a}-2\vec{b})\cdot \vec{b}}{|\vec{b}|}=\frac{-836}{\sqrt{1948}}[/m]
в)
[m]cos( ∠ \vec{a},(\vec{-2b}))=\frac{\vec{a}\cdot(\vec{-2b})}{|\vec{a}|\cdot |\vec{-2b}|}[/m]
[m]\vec{a}\cdot(\vec{-2b})=-2\cdot \vec{a}\cdot \vec{b}=-2\cdot 1020=-2040[/m]
[m]|\vec{a}|^2=\vec{a}\cdot \vec{a}=684[/m]
[m]|-2\vec{b}|^2=(-2\vec{b})\cdot(-2 \vec{b})=4\cdot \vec{b}\cdot \vec{b}=4\cdot 1948[/m]
[m]cos( ∠ \vec{a},(\vec{-2b}))=\frac{-2040}{\sqrt{684}\cdot \sqrt{4\cdot 1948}}=\frac{-1020}{\sqrt{684}\cdot \sqrt{1948}}[/m]