Задача 59796 ...
Условие
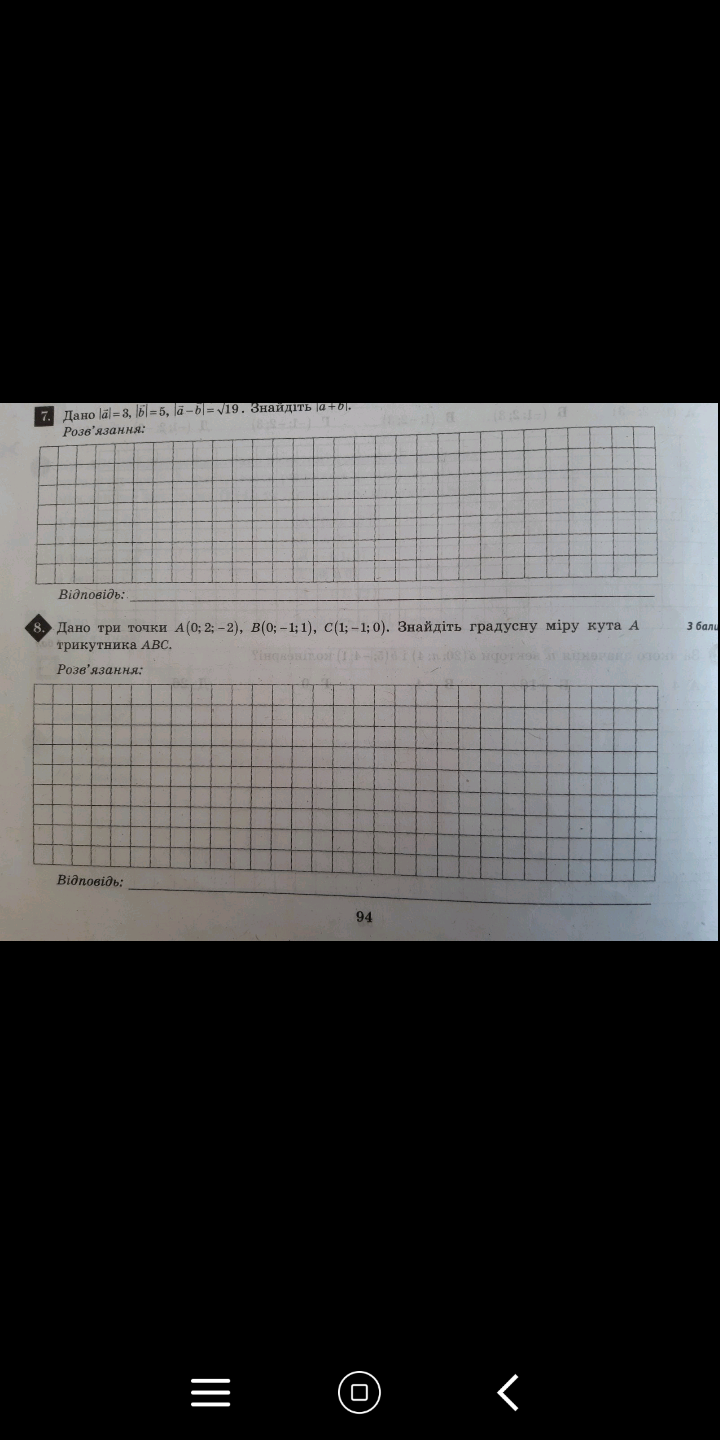
Решение
поэтому
[b]|(vector{a}-vector{b})|^2=(vector{a}-vector{b})*(vector{a}-vector{b})[/b]
⇒
Находим скалярное произведение:
(vector{a}-vector{b})*(vector{a}-vector{b})=
применяем законы векторной АЛГЕБРЫ (раскрываем скобки как в алгебре):
=vector{a}*vector{a}-vector{b}*vector{a}-vector{a}*vector{b}+vector{b}*vector{b}
Так как по условию
|vector{a}|=3
|vector{b}|=5
|vector{a-b}|=sqrt(19) ⇒ (vector{a}-vector{b})*(vector{a}-vector{b})=19
vector{a}*vector{a}=|vector{a}|*|vector{a}|*cos0=|vector{a}|*|vector{a}|
(vector{a}-vector{b})*(vector{a}-vector{b})==|vector{a}|*|vector{a}|-vector{b}*vector{a}-vector{a}*vector{b}+|vector{b}|*|vector{b}|
⇒
19=3*3-2vector{a}*vector{b}+5*5
⇒vector{a}*vector{b}=7,5
Находим скалярное произведение:
(vector{a}+vector{b})*(vector{a}+vector{b})=
=vector{a}*vector{a}+vector{b}*vector{a}+vector{a}*vector{b}+vector{b}*vector{b}=
=3*3+2*7,5+5*5=49
|(vector{a}+vector{b}|^2=49
|(vector{a}+vector{b}|=7
О т в е т. |(vector{a}+vector{b}|=7