Задача 55255 Хелп3.2.2...
Условие
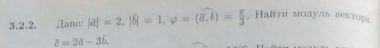
математика ВУЗ
645
Решение
★
[m]|\vec{c}|^2=\vec{c}\cdot \vec{c}[/m] ( см. приложение)
Находим скалярное произведение:
[m]\vec{c}\cdot \vec{c}= (2\vec{a}-3\vec{b})\cdot (2\vec{a}-3\vec{b})= [/m]
векторная АЛГЕБРА, поэтому как в алгебре раскрываем скобки:
[m]=4\vec{a}\cdot \vec{a}-12\vec{a}\cdot \vec{b}+9\vec{b}\cdot\vec{b}=4\cdot ( \vec{a})^2-12\cdot\vec{a}\cdot \vec{b}+9\cdot (\vec{b})^2 [/m]
скалярные квадраты: [m]( \vec{a})^2[/m] ; [m](\vec{b})^2[/m] и скалярное произведение [m] \vec{a}\cdot \vec{b}[/m]
[m]=4\cdot 2\cdot 2 -12 \cdot 2\cdot 1\cdot cos \frac {π}{3} + 9\cdot 1\cdot 1=[/m] .... считаем самостоятельно
О т в е т.[m] |\vec{c}|=\sqrt(\vec{c}\cdot \vec{c})=[/m]
