Векторы в пространстве

Дано 2 векторы a и b. |a|=13, |b|=19, |a-b|=22, найти |a+b|

Дан параллелепипед ABCDA1B1C1D1; AB=a AD=b,AA1=c разложите вектор AM по трем векторам a b и c если M=D1C DC1​

Даны векторы а⃗ , b⃗ и c⃗ . Необходимо: а) вычислить
смешанное произведение трех векторов; б) найти модуль
векторного произведения; в) вычислить скалярное произведение
двух векторов; г) проверить, будут ли коллинеарны или
ортогональны два вектора; д) проверить, будут ли компланарны
три вектора.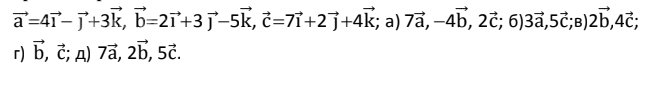

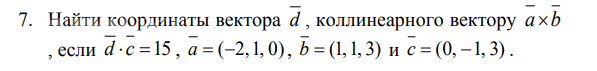
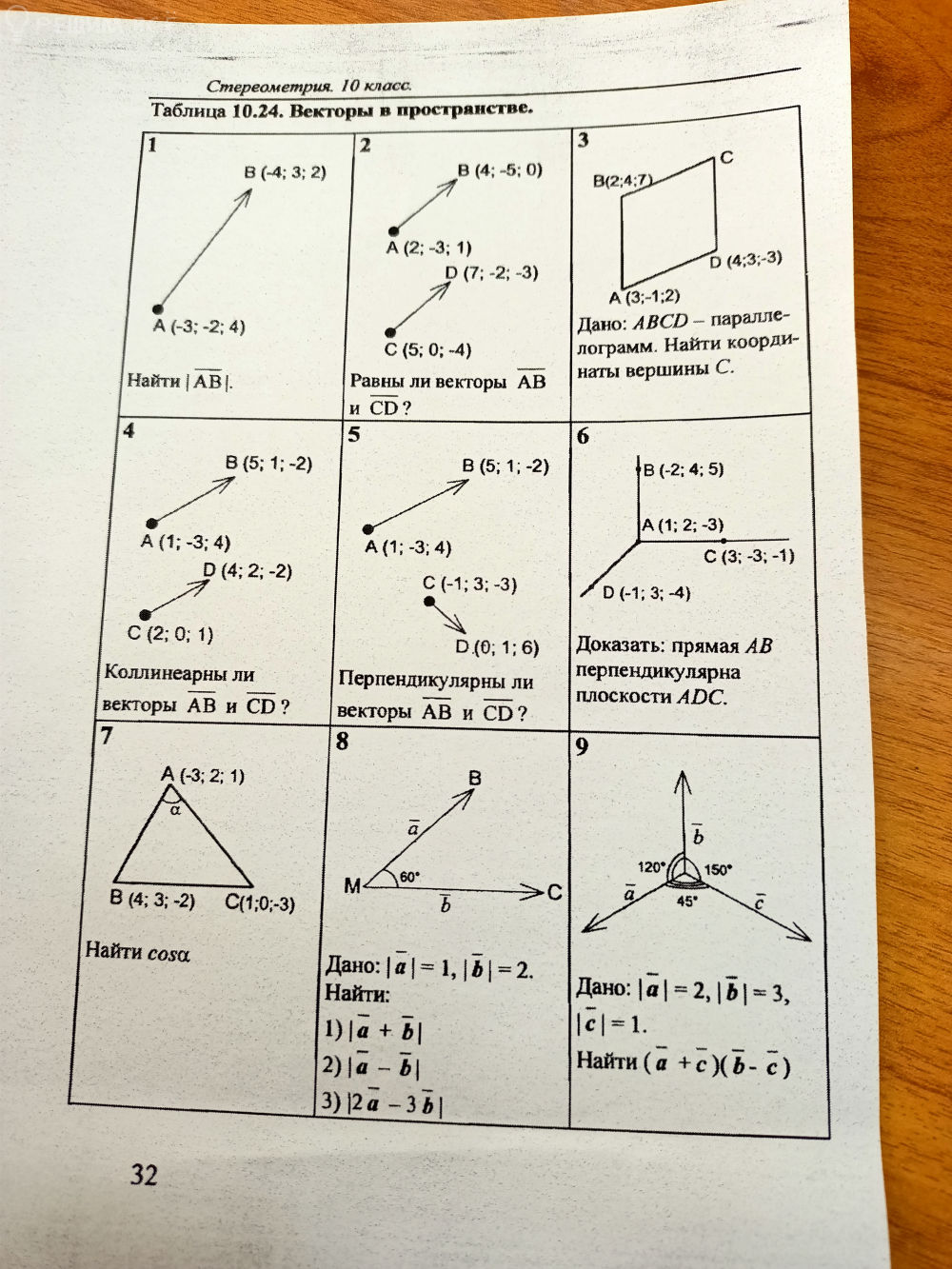
В базисе (e1, e2, e3) даны векторы a1 = (- 2; 1; 0) a2 = (1; 2; 1) и a3 = (- 3; - 1; 2) Найти координаты вектора d = e1 - 2e2 + 3e3 в базисе (a1, a2, a3)

разложить вектор а=2i-k по векторам е, (-1;0;0), е₂ (1;1;0), e, (1;1;1).

Найдите разложение a = xp + yq + zr вектора a по векторам p, q, r:

Даны векторы: вектор а(-3;-1;2), вектор с(5;-2;7). Найдите координаты вектора: вектор минус а+вектор 3с. ОТВЕТ (18;-5;19)

найдите косинусы углов вектора ē(1;1;1) с координатными векторами.

Дан параллелограмм ABCD, три вершины которого заданы. Найти четвертую вершину и острый угол параллелограмма. A(2;3;1) B(-4;2;3),C(-3;2;-4)

Найти координаты вектора а, коллинеарного вектору a x b „если dc=15 , а = (-2,1,0), b= (1, 1,3) и с= (0, -1, 3).

387. Построить вектор г = ОМ = 2i+ 3j + 6К и определить его длину и направление (проверить по формуле соs^2 α + соs^2 β +cos^2 γ )

№ 9. Вычислить проекции вектора & =2.АВ +3АС—5ВС на оси координат, если A (3, 3, 1), В 5 5, -2), С(4,1,1).

Написать решение трёх задач , ответ уже есть! Благодарю заранее

Стереометрия. 10 класс.
Таблица 10.24. Векторы в пространстве.

1
Найти |AB|.

2
Равны ли векторы AB и CD?

3
Дано: ΔBCD ― параллелограм. Найти координаты вершины C.

4
Коллинеарны ли векторы AB и CD?

5
Перпендикулярны ли векторы AB и CD?

6
Доказать: прямая AB перпендикулярна плоскости ADC.

7
Найти cosa

8
Дано: |a| = 1, |b| = 2.
Найти:
1) |a + b|
2) |a - b|
3) |2a - 3b|

9
Дано: |a| = 2, |b| = 3, |c| = 1.
Найти (a + c)(b - c)

Завдання 4. Обчислити об’єм тетраедра з вершинами в
точках
A1, A2, A3, A4 і його висоту, опущену з вершини
A4 на грань A1A2 A3 .
А1 (-1,-5,2), А2(-6,0,-3) , А3(3,6,-3), А4(-10, 6, 7)

При каком значении λ векторы
a=( λ , 3, 2 ) ,
|b|=(2, -3,-4)
и
c=(-3,12, 6)
будут компланарны?