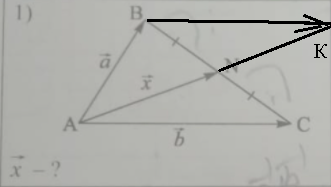
Задача 60473 Выразите векторами a и b....
Условие
Решение
[m]\vec{AK}=\vec{AB}+\vec{BK}=\vec{a}+\vec{b}[/m] ( см. рис)
[m]\vec{AK}=2\vec{x}[/m]
[m]2\vec{x}=\vec{a}+\vec{b}[/m]
[m]\vec{x}=\frac{1}{2}\vec{a}+\frac{1}{2}\vec{b}[/m]
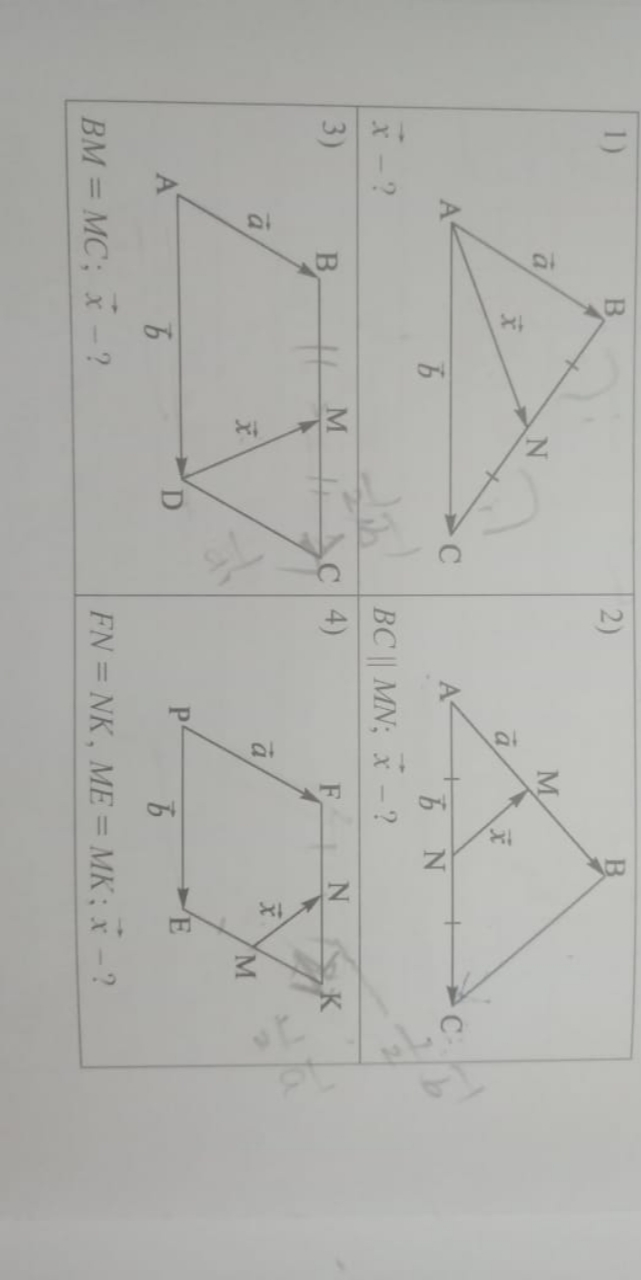
2.
[m]\vec{AM}+\vec{MN}=\vec{AN}[/m]
[m]\vec{a}-\vec{x}=\vec{b}[/m] ⇒[m]-\vec{x}=\vec{b}-\vec{a}[/m]
[m]\vec{x}=\vec{a}-\vec{b}[/m]
3.
[m]\vec{AB}+\vec{BM}+\vec{MD}=\vec{AD}[/m]
[m]\vec{BM}=\frac{1}{2}\vec{AD}=\frac{1}{2}\vec{b}[/m]
[m]\vec{a}+\frac{1}{2}\vec{b}-\vec{x}=\vec{b}[/m] ⇒
[m]\vec{x}=\vec{a}-\frac{1}{2}\vec{b}[/m]
4.
[m]\vec{PF}+\vec{FN}+\vec{NM}+\vec{ME}=\vec{PE}[/m]
[m]\vec{a}+\frac{1}{2}\vec{b}-\vec{x}-\frac{1}{2}\vec{a}=\vec{b}[/m] ⇒
[m]\vec{x}=\vec{a}+\frac{1}{2}\vec{b}-\frac{1}{2}\vec{a}-\vec{b}[/m] ⇒
[m]\vec{x}=\frac{1}{2}\vec{a}-\frac{1}{2}\vec{b}[/m]