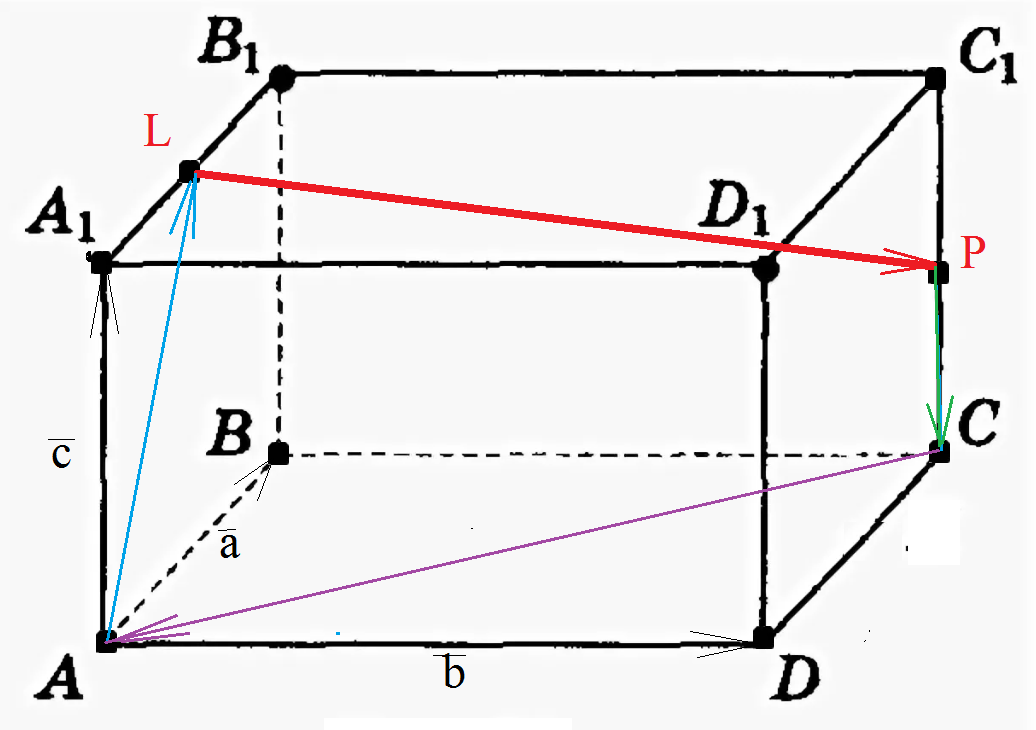
Задача 49298 В параллелепипеде АВСДА1В1Д1С1 точки L и...

a_luda_i

2020-05-05 10:05:22

В параллелепипеде АВСДА1В1Д1С1 точки L и Р являются серединами рёбер А1В1 и СС1 соответственно. Выразить вектор LP через вектора АА1, АВ и АД

sova

2020-05-05 10:53:13

★

vector{LP}+vector{PC}+vector{CA}+vector{AL}=vector{0}

Выразим векторы
vector{PC}
vector{CA}
vector{AL}
через
vector{AB}=vector{a}
vector{AD}=vector{b}
vector{AA_(1)}=vector{c}

vector{PC}=(1/2)vector{C_(1)C}= - (1/2)vector{c}

vector{CA}=-vector{a}-vector{b}, так как
vector {AC}=vector{AB}+vector{BC}=vector{AB}+vector{AD}

vector{AL}=vector{AA_(1)}+vector{A_(1)B_(1)}=vector{c}+(1/2)vector{a}

vector{LP} - (1/2)vector{c}-vector{a}-vector{b}+vector{c}+(1/2)vector{a}=vector{0}

vector{LP} + (1/2)vector{c}-(1/2)vector{a}-vector{b}=vector{0}

vector{LP}=(1/2)vector{a}+vector{b}-(1/2)vector{c}