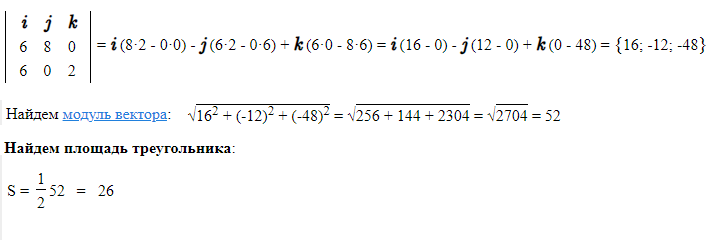Задача 35259 помогите решить пожалуйста срочно ...

vk280770680

2019-04-02 19:01:32

помогите решить пожалуйста срочно номер №3 №4 №5

sova

2019-04-02 19:17:05

★

5.vector{a} * vector{c}=|vector{a}| *|vector{c}|*cos( ∠ (vector{a}, vector{c})

cos( ∠ (vector{a}, vector{c})=(vector{a} * vector{c})/(|vector{a}| *|vector{c}|)=-3sqrt(2)/(2*|vector{a}|)=

|vector{a}|=?

4.
Пусть vector{b}=(x;y;z)
vector{a} коллинеарен vector{b}
Значит координаты векторов пропорциональны:
-1:х=2:у=2:z
vector{a} * vector{b}=-18
-x+2y+2z=18

Система
{-1:х=2:у=2:z
{-x+2y+2z=18
Обозначим
-1:х=2:у=2:z=k

x=-1/k
y=2/k
z=2/k

подставляем во второе уравнение:
(1/k)+(4/k) + (4/k) =18
4/k=18
k=4/18=2/9

x=-9/2
y=9
z=9

О т в е т. vector{b}=(-9/2;9;9)

3.
vector{MN}=(0-(-6);8-0;0-0)=(6;8;0)
vector{MT}=(0-(-6);0-0;2-0)=(6;0;2)

S(параллелограмма)=|vector{MN}×vector{MT}|

S_( ΔMNT)=(1/2)*|vector{MN}×vector{MT}|