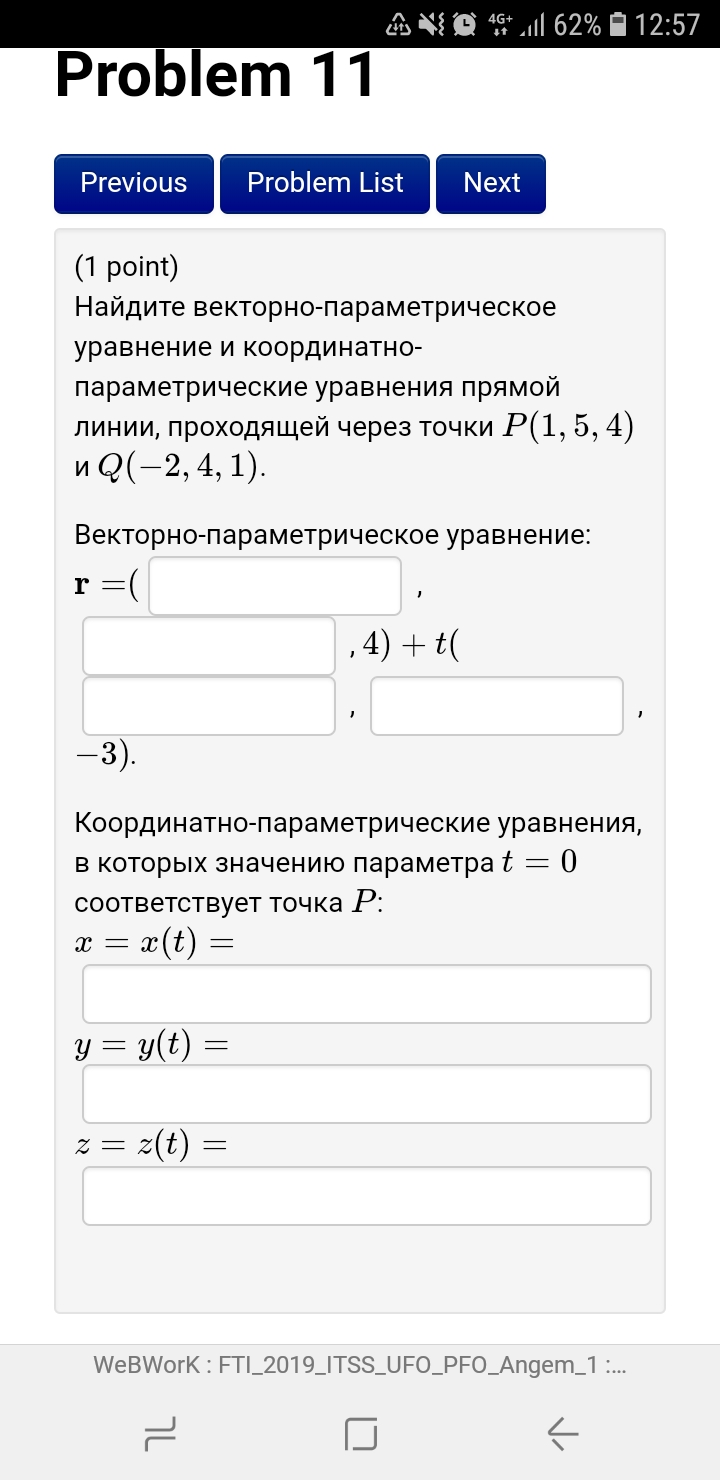
Задача 32874 Найдите векторно-параметрическое...

vk151256823

2019-01-21 10:52:25

Найдите векторно-параметрическое уравнение и координатно-параметрические уравнения прямой линии, проходящей через точки P(1, 5, 4) и Q(-2, 4, 1).

Векторно-параметрическое уравнение:
r = ( , , 4) + t ( , , -3).

Координатно-параметрические уравнения, в которых значению параметра t = 0 соответствует точка P:
x = x(t) =

y = y(t) =

z = z(t) =

sova

2019-01-21 12:00:12

★

Составляем уравнение прямой проходящей через две точки:
(x-1)/(-2-1)=(y-5)/(4-5)=(z-4)/(1-4)
(x-1)/(-3)=(y-5)/(-1)=(z-4)/(-3)
Параметризуем. Вводим параметр t
(x-1)/(-3)=(y-5)/(-1)=(z-4)/(-3)=[b] t[/b]
x=1-3t
y=5-t
z=4-3t

вектор{r}=(1;5;4)+t*(-3;-1;-3)
При t=0
получаем координаты точки Р