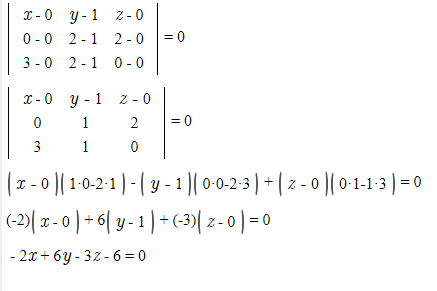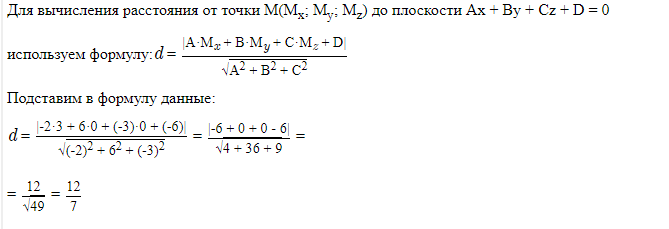Задача 32159 В прямоугольном пароллелепипеде...

vk483977274

2018-12-19 23:58:07

В прямоугольном пароллелепипеде ABCDA1B1C1D1
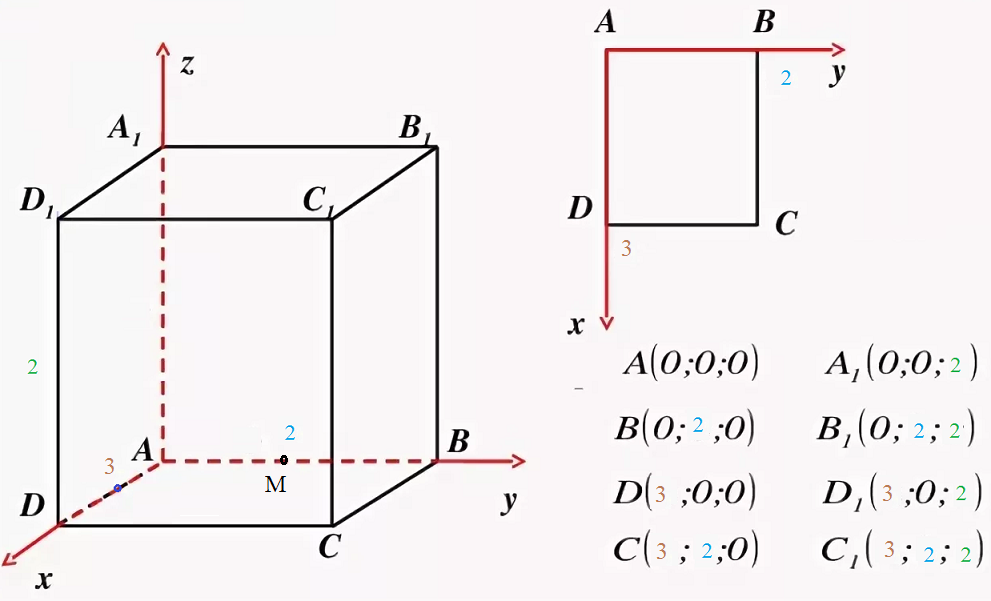
AB=AA1=2,BC=3,точка М- середина АВ
Найти :
а) длину отрезка МD1
б) угол между А1М и AD1
в) расстояние от точки D до плоскости В1СМ
г) угол между DM и плоскостью В1СМ
д) угол между плоскостями В1СМ и АСD1

sova

2018-12-20 08:09:45

Расположим параллелепипед в системе координат так как показано на рисунке.
Тогда вершины параллелепипеда имеют координаты ( см. там же)

a) M- середина АВ
M(0;1;0)
|MD_(1)|=sqrt((3-0)^2+(0-1)^2+(2-0)^2)=sqrt(14)
б)
vector{A_(1)M}=(0;1;-2)
vector{AD_(1)}=(3;0;2)

cos ∠ (vector{A_(1)M},vector{AD_(1)}) = (vector{A_(1)M}*vector{AD_(1)})/(|vector{A_(1)M}|*|vector{AD_(1)}|)=
=(0*3+1*0+(-2)*2)/sqrt(5)*sqrt(13)=-4/sqrt(65)
угол между векторами тупой,
cмежный угол - острый, его и принимаем за угол между прямыми.

∠ (A_(1)M},AD_(1)) = arccos(4/sqrt(65)

в)
Составляем уравнение плоскости
B_(1)CM
-2x+6y-3z-6=0