Задача 32871 Найдите векторно-параметрическое...
Условие
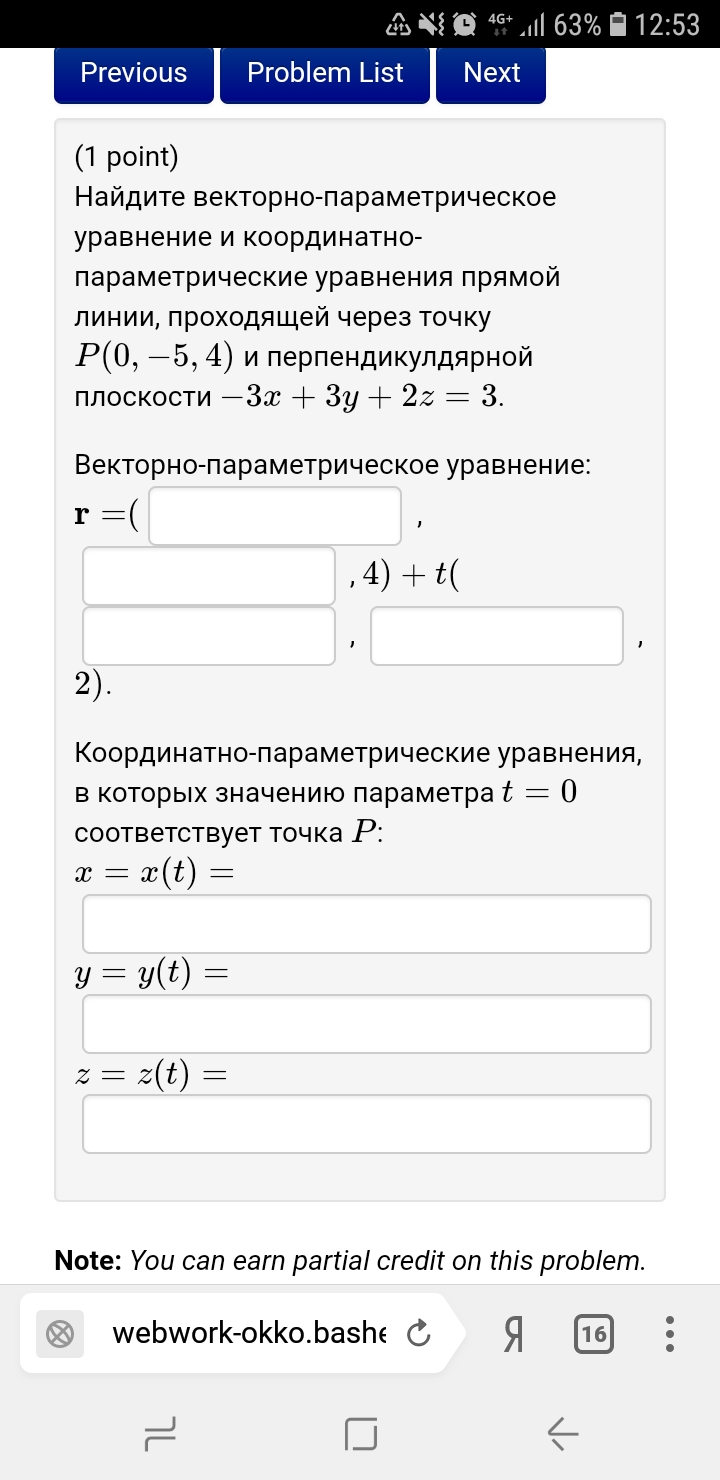
начерт
1059
Решение
★
Прямая перпендикулярна плоскости, значит нормальный вектор плоскости есть ее направляющий вектор
Составляем уравнение прямой, проходящей через точку Р(0;-5;4)
с направляющим вектором vector{n}=(-3;3;2)
(x-0)/(-3)=(y+5)/3=(z-4)/2
Параметризуем.
Вводим t:
(x-0)/(-3)=(y+5)/3=(z-4)/2=t
x=0-3t
y=-5+3t
z=4-2t
в векторно-параметрическом виде
vector{r}=(0;-5;4)+t*(-3;3;2)
