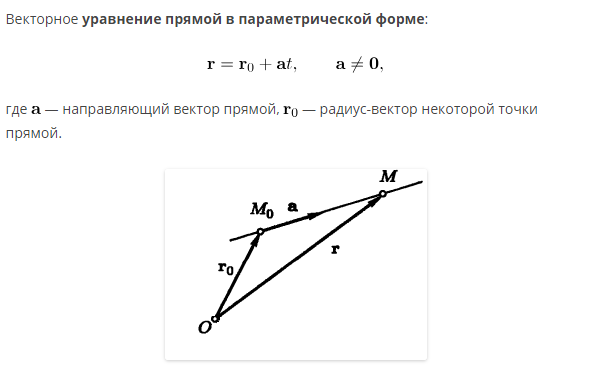
Задача 32784 Найдите векторно-параметрическое...
Условие
Векторно-параметрическое уравнение:
[m]
\mathbf{r} = \left( \begin{array}{c} \\ \\ \end{array} \right) + t \left( \begin{array}{c} \\ \\ \end{array} \right)
[/m]
Координатно-параметрические уравнения, в которых значению параметра [m] t = 0 [/m] соответствует точка [m] P [/m]:
[m]
x = x(t) =
[/m]
[m]
y = y(t) =
[/m]
[m]
z = z(t) =
[/m]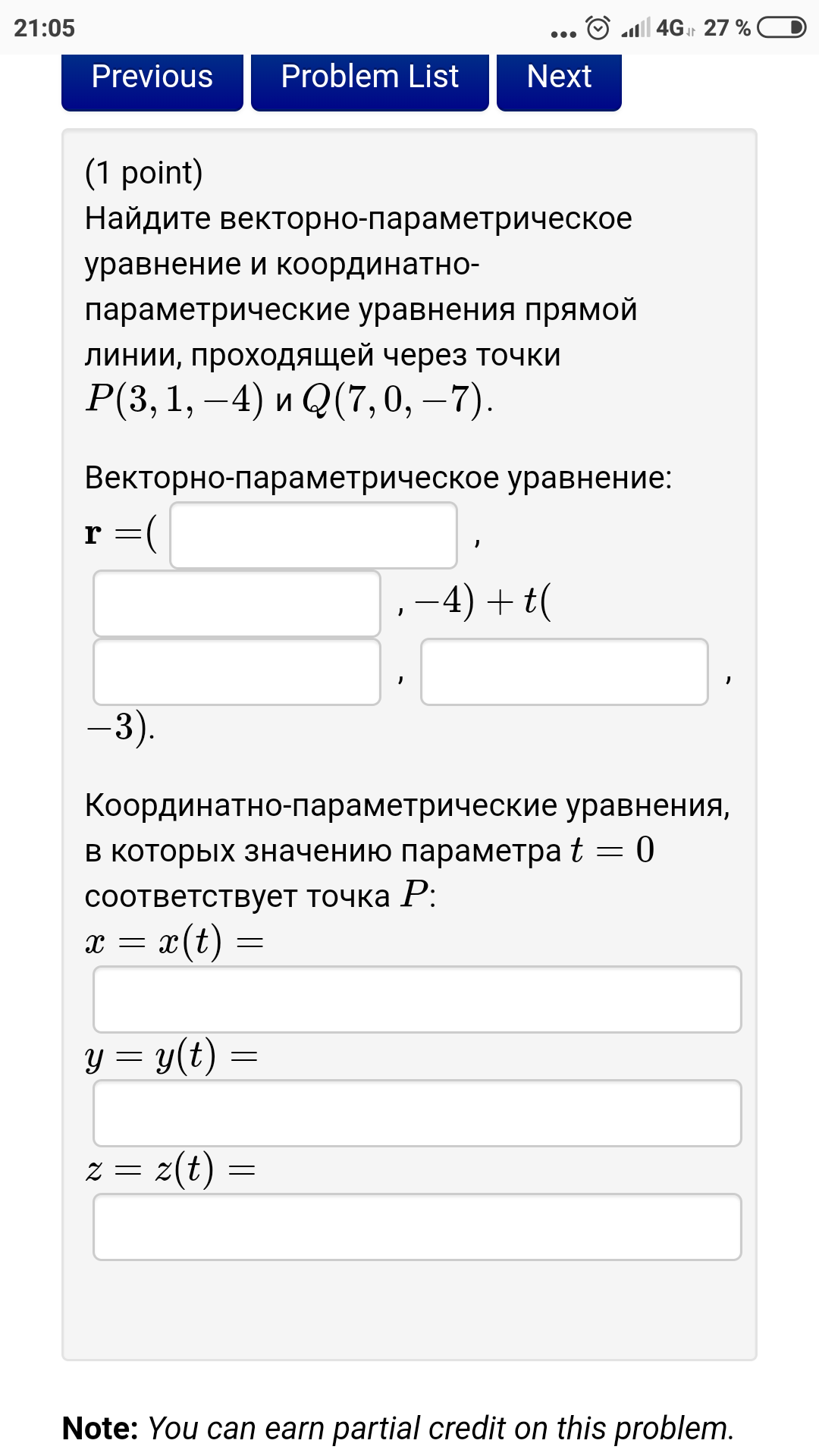
Решение
Q это М
vector{a}=(7-3;0-1;-7-(-4))=(4;-1;-3)
vector{r}=vector{r_(o)} + t*vector{a}=
=(3;1;-4)+ t*(4;-1;-3)
x=x(t)=3+4t
y=y(t)=1-1t
z=z(t)=-4-3t
при t=0
x=-3
y=1
z=-4
и есть координаты точки Р