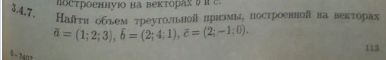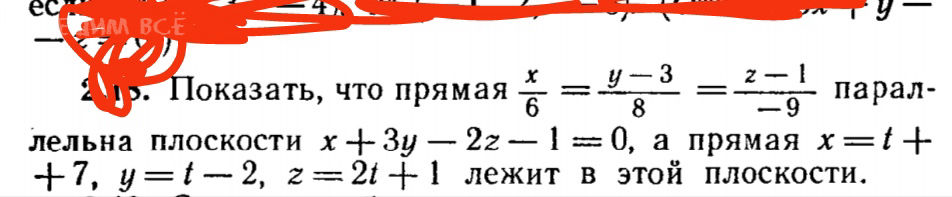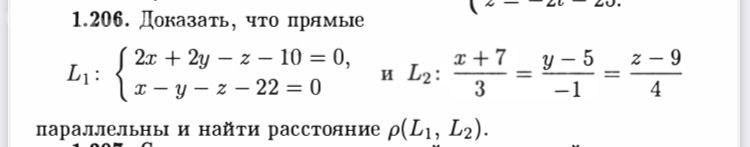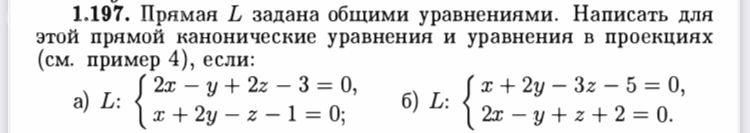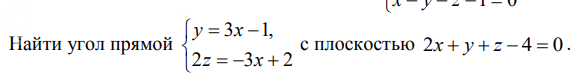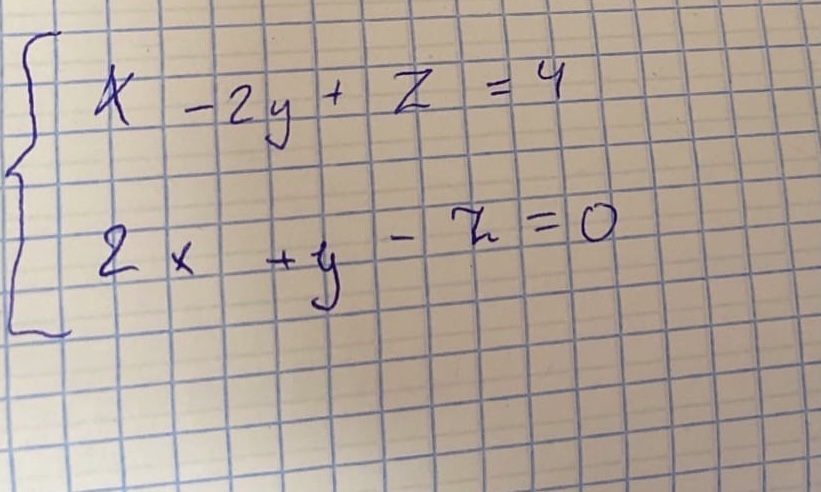В пространстве

кто может решить вообще не знаю что да как, буду очень благодарен

Составить уравнение плоскости Р, проходящей через точку А
перпендикулярно вектору

BC
. Написать ее общее уравнение, а также
нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить
уравнение плоскости
P1
, проходящей через точки А, В, С. Найти угол между
плоскостями Р и
P1
. Найти расстояние от точки D до плоскости Р
А(0;2;-1) В(-1;2;3) С(-2;3;-1) D(0;4;1)

©< у —- @. !!оказать, что прямая % =_у_;і =i_:9—l napan- лельна плоскости х -- Зу — 2г — 1 == 0, а прямая х = Ё +-7, у== — 2, г==21--| лежит в этой плоскости.

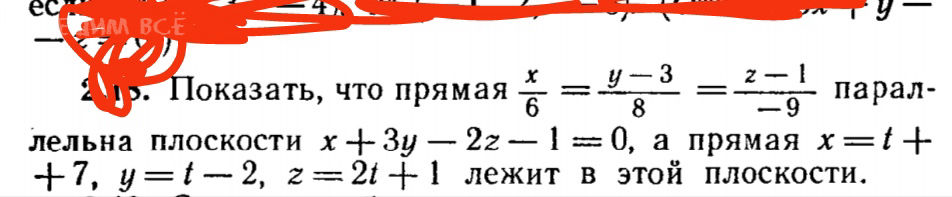
Найти точку B, симметричную точке A (1;2;0) относительно плоскости 2x–3y+5z=5

4. Найти ;пш\п›‹ив от прямой. | х=-21,у=9!-7,2 = 21+2 ло прямой, | проходящей через точку M(9,-2,0) параллельно | плоскостям х+ у-2+3-0 н Tx+5y+2z-1=0. \

Составить параметрические уравнения прямой, проходящей через точки пересечения плоскости Эх+ у -Зг +1= 0 с прямыми PR =5 [z-1 x=5 _y-3 _z+4 1 -5 2 2 4 -6 ° | `Найти угол между искомой прямой и первой | ‚данной прямой. i |

Написать уравнение плоскости проходящей через точку M1(2;0;-1) M2(-3;1;3) параллельно к вектору s=(1;2;-1)

При каких значениях коэффициентов А и В плоскость Аx + Вх +6z -7=0 перпендикулярно к прямой x-2/2 = y+5/-4 = z/3 ?
Найти орт. вектора нормали плоскости

Доказать, что прямые L1 и L2 параллельны и найти расстояние p(L1, L2).

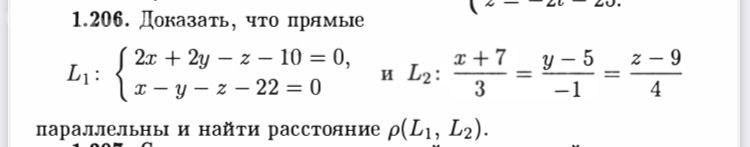
Прямая L задана общими уравнениями.Написать для этой прямой канонические уравнения и уравнения в проекциях,если…

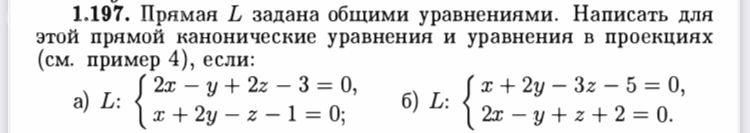
Найти угол прямой заданой системой с плоскостью

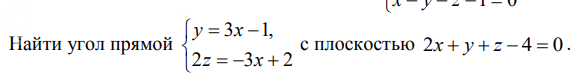
Даны точки М1(-6;-3;-1), М2(8;7;-3) и плоскость
Р: 9x-4y+9z-11=0. Найти уравнение плоскости, проходящей через точки
М1, М2 и перпендикулярной плоскости Р.

задача 4, задание 3
Найти точку М ,симметричную точке М относительно прямой (для вариантов 1-15) или плоскости (для вариантов 16-25)

Задача 5, задание 3
Найти точки пересечения поверхности и прямой

Найти координаты точки А, равноудаленной от точек B b и С
А(0,0,z) , B(3,3,1), С(4,1,2)

Составить уравнение плоскости проходящей через точку М(2,3,4) параллельно двум данным векторам a= 2i-3j+4k и b= -3i+4j+2k

Даны плоскость π и прямая l. Найти точку их пересечения. Составить
векторное параметрическое уравнение ортогональной проекции m прямой l на
плоскость π, взяв в качестве опорной точки точку пересечения.

[r][b]π: 171x − 35y − 434z − 741 = 0; l: x = −4 − 6t, y = 3 + 2t, z = 4 + 5t[/b][/r]

уравнение плоскости проходящей через прямую и перпендикулярна к плоскости

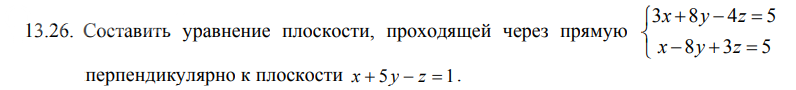
4. Прямая проходит через точки — 4А(2;-1;3) и В(0;2;-1). Найдите точку пересечения этой прямой с плоскостью Зх-у+z= 0.

4. Даны три последовательные вершины параллелограмма: А(2;4;3), В(-3; 0; 6), С(-4; 2; 1). Найти уравнения стороны AD и диагонали BD.

Уравнение плоскости, проходящей через точки A(3;0;0) B(0;2;0) C(0;0;1).

Даны точки Мо (-21; 20; —16), М1 (-2; —1; —1), М2 (0; 3; 2), М3 (3; 1; —4). Составить уравнения а) плоскости MiMaMs; 6) прямой М\Мё; в) прямой Мы, перпендикулярной к плоскости М МэМз; г) прямой МуМ, параллельной прямой М)М.

через точку M(1,5,-1) провести прямую перпендикулярную к прямым
2x-y+3z+4=0
-x+2y+2z-2=0



x-y-z+1=0
2x+y+4z=0

На плоскости Oxz найти такую точку Р, разность расстояний которой до точек M1(3; 2; -5), М2(8; -4; -13) была бы наибольшей.

4вопрос нужно решать

1. Определите, какие из M1 (N; 2; 4), M2 (6; 1; -n), M3 (2; -7; 7) лежат на плоскости 2x + 7Y + Z +12 = 0.

Найти уравнение плоскости, проходящей через точку M0 (1;-7;4) параллельно векторам (3;1; -2), (2;2;1).

8.При каких значениях B и C плоскости 6x + By – 9z + 7 = 0 и 2x – y + Cz + 7 = 0 параллельны?

9. При каком значении A плоскости 3x + 2y + 5z – 7 = 0 и Ax + 2y + z – 4 = 0 перпендикулярны?

10. Найти расстояние от точки M(3;3;-7) до плоскости 6x + 4y + 3z +10 = 0 .

найти точку пересечения прямой плоскости (N=7)

найти точку пересечения прямой… с координатными плоскостями
(N=7)

Напишите уравнения плоскости, проходящей через точку М (5; -1; 0) перпендикулярно вектору n =(0; -6; 10)

Знайдіть площу трикутника АВС використавши формулу
S=½×a×b×sinà
якщо : А(2;1;9) В(-2;3;4) С(3;1;1)

В параллелепипеде ABCD A'B'C'D' координаты вершин A(6,5,-4) B(3,1,0) C(-1,-1,0) A'(-1,1,1) Найти координаты вершины D

4.231.постройте канонические уравнения медианы EL треугольника, вершины которого лежат в точках Е(2;3;-1), F(1;-2;0) Q(-3;2;2).

Объем треугольной призмы равен 9. Три его вершины находятся в точке А(4;-1;2), B(5;1;4),C(3;2;1). Найдите координaты четвертой вершины D , если она находится на оси Оy

Написать уравнение перпендикуляра, опущенного с точки М(2;1;0) на прямую
{x=3z-1, y=2z}

уравнение плоскости, проходящей через точку А и перпендикулярной прямой АВ, если А(-1,2,1), В(-3,1,-2)

Знайдіть координати точки у яку точка А(3;-2;1;) у наслідок симетрії відносно точки В(-1;2-1;)

На осе ОУ найдите точку, равноудаленную от т.А(8,4,-2) и В(-2,6,4)

Найти координаты центра и радиус сферы, которая проходит через точки А(0;1;-1), B(1;0;1), C(-1;1;0), D(1;-1;1).

. Прямую, заданную как пересечение плоскостей 2х + у - 2z - 1=0 и 3х - 2у + 3z - 2=0, представить как пересечение таких двух плоскостей, из которых одна параллельна оси Ох, а другая параллельна оси Оz.

Точки А(1:1; 4), В(2: 3: 1), (-2; 2; 0) — вершини парвлелограма ABCD. Знайдіть координати вершини D.

Найти проекцию точки А (3;2;1) на прямую даю 100 баллов

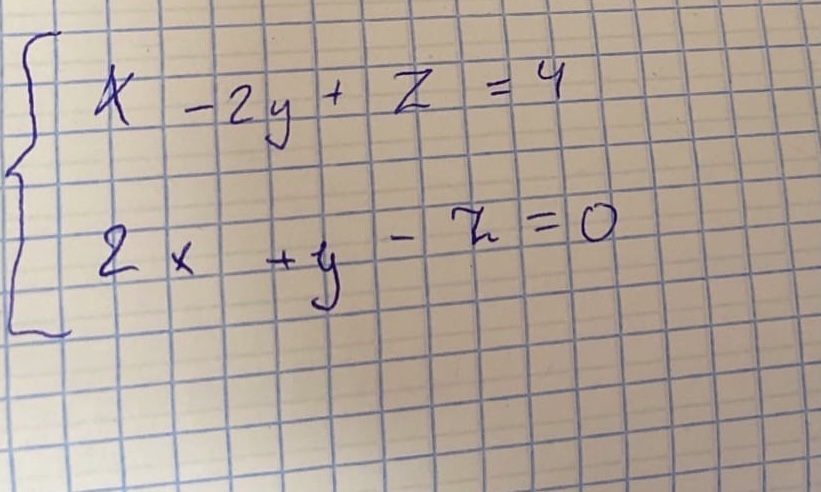
Составить уравнение плоскости O проходящей через точку A(3;-2;5) и образующей угол П/6 с плоскостью I, проходящей через точки B(0;0;1) С(0;5;0) D(1;0;0). Плоскость содержит прямую AB

1. Найти площадь ∆ABC и угол в точке A, если координаты точек
A(-2,-2,0), B(-1,-2,4), C(4,0,4)

2. Составить уравнение плоскости, проходящей через начало координат и перпендикулярно к вектору AB. если A(5,-2,3), B(1,-3,5).

Написать уравнение плоскости, проходящей через точки M1(1; 0; – 1), M2(–3; 1; 3) параллельно вектору s = (1; 2; –1).

Номер 3, помогите пожалуйста. Очень срочно для экзамена. Даю 100б

Умоляю, помогите решить эти два задания????
Пожалуйста ????????????????????????

Составить уравнение плоскости, проходящей через ось Oy и точку A( 1;3; 3)   .

найдите точку симметричную точке А(1,2,-3) относительно плоскости x-2z+2

3. Составить уравнения плоскости, проходящей через:
1) ось Oz и точку A(2; -3; 4);
2) точку A параллельно плоскости Oxy.

Составить уравнение плоскости, расположенной на расстоянии четырех единиц от плоскости 3x–6y–2z+8=0 и параллельно ей.

Найти уравнение плоскости, которая проходит через точки А (2, 5, -1), В (-3, 1, 3) параллельно оси Оy.

Дан треугольник с вершинами А(-3,-2,0), В(3;-3;1), С (5;10;2). Найти длину высоты АД треугольника АВС.

4. Составить уравнение плоскости, параллельной оси Oz и проходящей через точки M₁ (3; −1; 2) и M₂ (−2; 3; 4).

Составить уравнение плоскости,проходящей через:
1)точку А(5;–4;6) перпендикулярно оси Ox
2)Точку А и отсекающей равные отрезки на координатных осях

Определить величины углов между осями координат и прямой x-2/-1=y+4/√2=z-1/1

5.2.9)Написать уравнение плоскости,проходящей через точку M(1;-1;0) , параллельно векторам a=(0;2;3) и b(-1;4;2)

Составить уравнение плоскости , проходящей через точки M1(-2;0;0),M2(0;4;0),M3(0;0;5)

Составить уравнение прямой, проходящей через точку
M(1; -1;2) и перпендикулярной векторам а= (2;2;3) и б =
= (-2;5;0).

Составьте канонические уравнения прямой , которая проходит через точку А(4;0;–1) и пересекает прямые

Определить вид поверхности и построить ее в каждой из следующих случаев:
А) х^2+2у^2--4y-2z=0
B)z^2+y^2-2z=0

Через точку B(5;0;1) провести прямую, параллельную плоскостям 2x + 3y - z + 4 = 0 и x + 4y + 2z - 3 = 0 .

На оси Oy найти точку M, равноудаленную от точек А(1; -4; 7) и В(5; 6; -5).

Даны вершины треугольника A(3; -1; 5), B(4; 2; -5), C(-4; 0; 3). Найти длину медианы, проведенной из вершины A.

Даны точки A 4,2,6 , B 2, 3,0 , C 10,5,8 , D 5,2, 4а.Площадь ABC

Вершины тетраэдра АВСD имеют координаты А( - 2; 0; 1) В( - 1; 2; 3), С (8; - 4; 9), D( 4; 6: 0).
а) Найдите координаты точки М — середины отрезка АС
б) Найдите длину медианы медианы DМ треугольника АСР
для проф уровня № 14) Определите расстояние между прямыми АВ и СD.

Даны точки А(-1; 5; 3), В(7; -1; 3), С(3; -2; 6).

а) Докажите, что треугольник АВС — прямоугольный.

б) Пусть а{а1; а2; а3} и b{b1; b2; bЗ} некоторые векторы с соответствуюЮЩиИМиИ координатами. Используя формулу а {а1; а2; а3 } * b{b1; b2; bЗ} = а1* b1+ a2* b2+ a3* b3, найдите произведение векторов АС и ВС

Определить координаты концов отрезка, который точками С(2:0:2) и D(5:-2:0) разделен на 3 равные части.

Даны точки А(3,0,-3), B(1,2,3), C(2,-2.1). Вычислить площадь треугольника АВС.

14. Построить плоскости:
a) 3x + 2y + z = 6; b) 3x + 2y + z = 0; c) 3x + 2y = 6; d) 3x - z = 0; e) z = 6.

16. Составить уравнение плоскости, зная, что точка P(3;-6;2) служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.

Даны координаты вершин пирамиды: A 1;4;3 , B 2;3;1 , C -2;1;3 , D 0;1;2.
Вычислить:
1. объём пирамиды;
2. длину ребра AB;
3. площадь грани ABC;
4. угол между ребрами AB и AD.

Точка M делит отрезок AB пополам. Найти точку B, если
известны точки A(2;0;-3),M(5;-4;1)

1. Вершины тетраэдра ABCD имеют координаты А( - 2; 0; 1) В(- 1; 6; 0), С (8; -4; 9), D (4; 6; 0).
a) Найдите координаты точки М - середины отрезка АС
б) Найдите длину медианы медианы DM треугольника ACD.

Даны точки A(-1; -5; 3), B(7; -1; 3), C(3; -2; 6).
а) Докажите, что треугольник ABC — прямоугольный.
б) Пусть а{a1; a2; a3} и b{b1; b2; b3} некотрые векторы с соответствующими координатами. Используя формулу а{a1; a2; a3}* b{b1; b2; b3}= a1* b1 + a2* b2+ a3* b3, найдите произведение векторов AС и ВС.

Даны четыре точки А1(х1, у1, z1), А2(х2, у2, z2), А3(х3, у3, z3), А4(х4, у4, z4). Составить уравнения:
а) плоскости А1А2А3;
б) прямой А1А2;
в) прямой А4М;
г) прямой А3К, параллельной прямой А1А2;
д) плоскости, проходящей через точку А4 перпендикулярно к прямой А1А2.

А1(4, 1, 2), А2(1, 2, 0), А3(3, 5, 7), А4(2, 3, 5)

Написать уравнение плоскости, проходящей через точку А
перпендикулярно плоскости α и параллельной вектору ????⃗ .
A(2;-1;9) α (2x-13y+z-2=0) ????⃗(2;-2;3)

Записать каноническое и параметрическое уравнения прямой,
проходящей через точку М и параллельной прямой L. M(5;-7;1)
L: система 30x+21y+19z+2=0
x-3z+1=0

Составить уравнение плоскости если DMN где M – середина АВ, а N– середина AC если А(1,–2, 1) В(0,2,5) С(–1,–1,1) D(1,0,3)

Найдите углы, периметр и площадь треугольника, вершинами которого являются точки A (1; -1; 3), B (3; -1; 1) и C (-1; 1; 3).

Вычислить:
е) синус угла между прямой А1А4 и плоскостью А1А2А3;
ж) косинус угла между координатной плоскостью Оху и плоскостью А1А2А3.
А1(4, 1, 2), А2(1, 2, 0), А3(3, 5, 7), А4(2, 3, 5)

составить уравнение плоскости проходящей через линию пересечения плоскостей х+2у+3z-5=0 и 3х-2у-z+1=0 и отсекающей равные отрезки на осях Ох и Оz

Найти точку А, симметричную точке B(2; 1; 0) относительно прямой

{ x = 2
{ y+z+2 = 0

Найти координаты точки пересечения плоскости, проходящей через точки А = (4;-3;-2), B=(14;-9:-6), C=(3;-2;-1) с прямой, проходящей через точки D=(21,-12,-9), E=(9,-6,-3)

Найти координаты точки, симметричной точке А=(-6,-6,10) относительно плоскости ,заданной уравнением 2*x+3*y-3*z-6=0.

Найти координаты точки, симметричной точке A = (6, —5, —9) относительно плоскости, заданной уравнением 2*x-1*y-3*z-2 = 0.

Найти координаты точки, симметричной точке A = (1, -4, -3) относительно плоскости, заданной уравнением -2 * x - 3 * y - 2 * z + 1 = 0.

Найти координаты точки пересечения плоскости, проходящей через точки А = (4; 1; 3), В = (8; 3; 1), С = (3; 0; 4) с прямой, проходящей через точки D = (25; 18; -9), Е = (—8; —15; 13).

Найти координаты точки пересечения плоскости, проходящей через точки A = (2; 1; 2), B = (10; 7; 6), C = (3; 2; 3) с прямой, проходящей через точки D = (-21; -15; -10), E = (6; 3; 8).

Провести плоскость через перпендикуляры, опущенные из точки A(-3;2;5) на плоскости 4x+y-3z+13=0 b x-2y+z-11=0

Записать уравнение и определить вид поверхности,полученной при вращении данной линии вокруг указанной оси координат,сделать рисунок
x2=–3z ; Oz.

На расстоянии двух единиц от плоскости x-6y-z+14=0 проведена
параллельная ей плоскость. Написать ее уравнение.

Составить канонические уравнения прямой, проходящей через точку
(0;7;4) параллельно оси OX.

Найти проекцию прямой (x–2)/5 = (y–3)/1 = (z+1)/2 на плоскость x+4y–3z+7=0

8. Лежат ли точки A(-1, -1, -1), B(-2, 1, -2), C(-1, 0, -2) и D(3, 2, 1) в одной плоскости?

9. Определить острый угол между высотой и медианой треугольника ABC, проведенными из вершины A, если координаты вершин известны: A(-2, 3), B(5, 7) и C(-3, -2).

12. Составить параметрические и канонические уравнения прямой, заданной как пересечение двух плоскостей: [m]2x - y - z - 1 = 0[/m] и [m]x + 2y + z - 2 = 0[/m].

13. Найти проекцию точки [m]A(1, 2, -3)[/m] на прямую, заданную как пересечение двух плоскостей: [m]- x + y - 2z + 1 = 0[/m] и [m]y + 4z + 2 = 0[/m].

Определить вид поверхности и построить эту поверхность:
а) 6x^2+y^2+6z^2-18=0
б) 3x^2+y^2-3z=0

Написать канонические уравнения прямой:

{ x + y - z + 2 = 0,
{ 4x - 3y + z - 1 = 0.

Составить уравнение плоскости, проходящей через точки А (2, 5, -1) и В (-3, 1, 3) параллельно оси Оу

Найти объем треугольной призмы, построенной на векторах