Задача 66723 При каких значениях коэффициентов А и В...

6367f441ad8c9721f0e6413a

06.11.2022 22:20:49

При каких значениях коэффициентов А и В плоскость Аx + Вх +6z -7=0 перпендикулярно к прямой x-2/2 = y+5/-4 = z/3 ?
Найти орт. вектора нормали плоскости

5f3ea7e3faf909182968ddd9

06.11.2022 23:52:23

★

плоскость
Аx + Вх +6z –7=0 задана общим уравнением
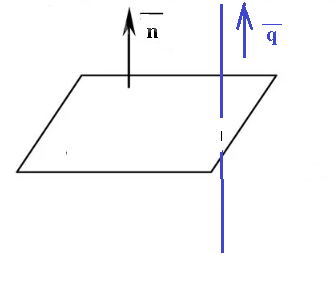
нормальный вектор vector{n}=(A;B;6)

прямая
(x–2)/2 = (y+5)/(–4) = z/3 задана каноническим уравнением

направляющий вектор прямой

vector{q}=(2;-4;3)

Прямая и плоскость перпендикулярны.

Значит, нормальный вектор vector{n}=(A;B;6) и направляющий вектор прямой

vector{q}=(2;-4;3) коллинеарны.

Координаты векторов пропорциональны:

A:2=B:(-4)=6:3

⇒
A:2=6:3 ⇒ [b]А=4[/b]
B:(-4)=6:3 ⇒ [b]В=-8[/b]

vector{n}=(4;-8;6)

|vector{n}|=sqrt(4^2+(-8)^2+6^2)=sqrt(116)=2sqrt(29)


vector{e}=(4/2sqrt(29); -8/2sqrt(29); 6/2sqrt(29))

vector{e}=(2/sqrt(29); -4/sqrt(29); 3/sqrt(29))- орт