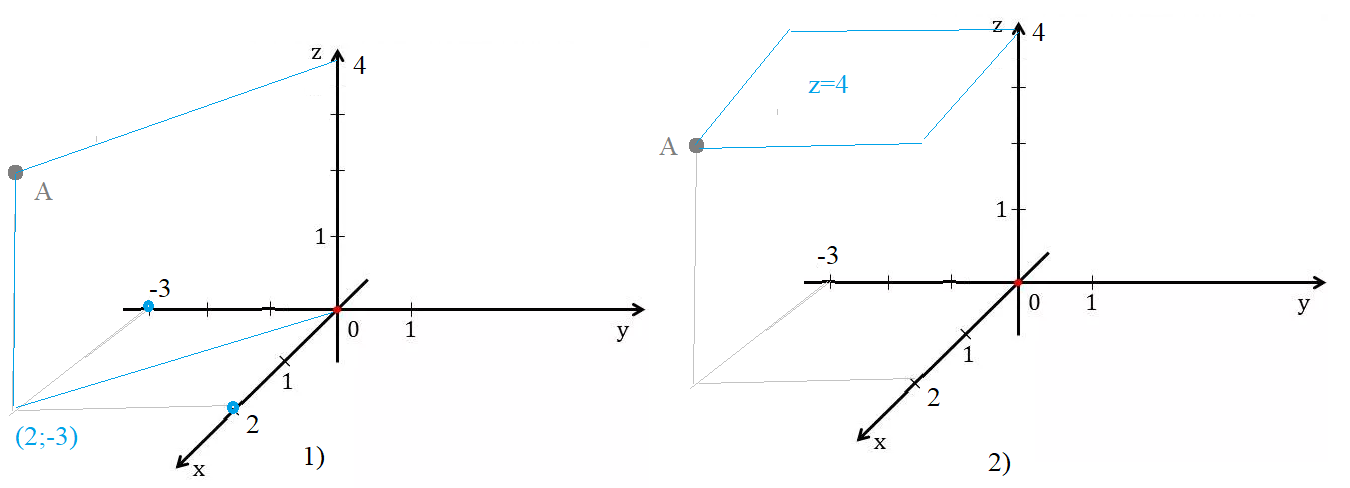
Задача 56531 3. Составить уравнения плоскости,...

Тёма_225699918

25 декабря 2020 г. в 09:32

3. Составить уравнения плоскости, проходящей через:
1) ось Oz и точку A(2; –3; 4);
2) точку A параллельно плоскости Oxy.

exponenta

25 декабря 2020 г. в 09:51

★

1)
Это плоскость, проходящая через начало координат ⇒ Значит ее уравнение имеет вид

ax+by+cz=0

Плоскость проходит через точку (0;0;1)

Значит

a·0+b·0+c·1=0

с=0


Плоскость проходит через точку A(2;–3;4)

a·2+b·(–3)+0·4=0


a·2+b·(–3)=0

⇒ a=(3/2)b

(3/2)bx+by=0

Делим на b

$3x+2y=0$

2)
$z=4$