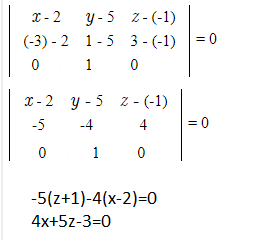Задача 31180 Составить уравнение плоскости,...

vk132396093

2018-11-21 11:19:07

Составить уравнение плоскости, проходящей через точки А (2, 5, -1) и В (-3, 1, 3) параллельно оси Оу

sova

2018-11-21 11:40:13

★

Пусть точка M(x;y;z) - произвольная точка плоскости.

Тогда векторы
vector{AM}; vector{AB} и vector{j} компланарны.
Условие компланарности трех векторов- равенство 0 определителя третьего порядка, составленного из координат векторов.
vector{AM}=(х-2;y-5;z-(-1))=(x-2;y-5;z+1)
vector{AB}=(-3-2;1-5;3-(-1))=(-5;-4;4)
vector{j}=(0;1;0)