Задача 65256 Уравнение плоскости, проходящей через...
Условие
Решение
ax+by+cz+d=0
Подставляем координаты точки А:
a*3+b*0+c*0+d=0 ⇒ 3a+d=0
Подставляем координаты точки B:
a*0+b*2+c*0+d=0 ⇒ 2b+d=0
Подставляем координаты точки C:
a*0+b*0+c*1+d=0 ⇒ c+d=0
Решаем систему трех уравнений:
[m]\left\{\begin {matrix}3a+d=0\\ 2b+d=0\\ c+d=0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}a=-\frac{d}{3}\\ b=-\frac{d}{2}\\ c=-d\end {matrix}\right.[/m]
Тогда
ax+by+cz+d=0 принимает вид:
(-d/3)x+(-d/2)y-dz+d=0
или
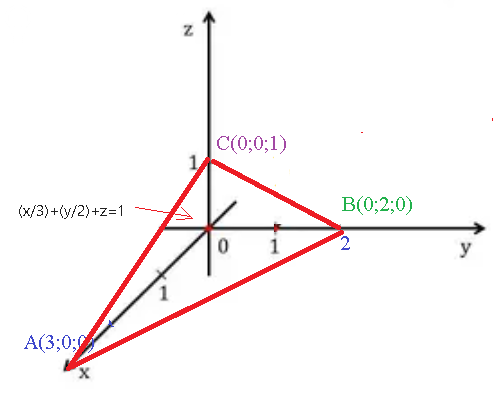
(x/3)+(y/2)+z=1 получили уравнение плоскости в отрезках, которые плоскость отрезает на координатных осях
на оси Ох 3
на оси Оу 2
на оси Оz 1
Все решения
[m]\begin{vmatrix}
x - xA & y - yA & z - zA\\
xB - xA & yB - yA & zB - zA\\
xC - xA& yC - yA & zC - zA
\end{vmatrix} = 0[/m]
В нашем случае: A(3; 0; 0); B(0; 2; 0); C(0; 0; 1):
[m]\begin{vmatrix}
x-3 & y-0 & z-0\\
0-3 & 2-0 & 0-0\\
0-3 & 0-0 & 1-0
\end{vmatrix} = 0[/m]
Упрощаем:
[m]\begin{vmatrix}
x-3 & y & z\\
-3 & 2 & 0\\
-3 & 0 & 1
\end{vmatrix} = 0[/m]
По правилу решения определителей:
(x - 3)*2*1 + y*0(-3) + z*0(-3) - (x - 3)*0*0 - y*1(-3) - z(-3)*2 = 0
Раскрываем скобки и упрощаем:
2x - 6 + 0 + 0 - 0 + 3y + 6z = 0
Ещё упрощаем:
2x + 3y + 6z - 6 = 0
Разделив всё на 6, получим уравнение в отрезках:
x/3 + y/2 + z = 1