Задача 66795 Прямая L задана общими...
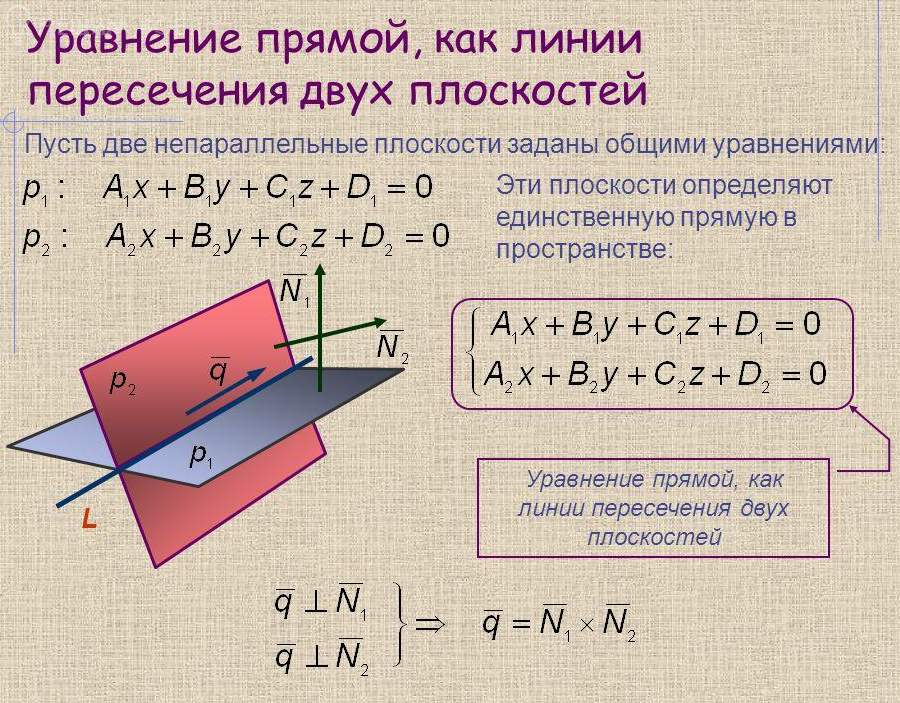
Условие
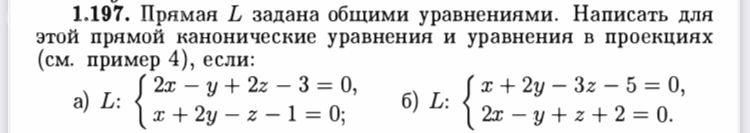
Решение
x+2y-z-1=0 - общее уравнение прямой с нормальным вектором vector{N_(2)}=(1;2;-1)
[m]\vec{q}=\begin {vmatrix} \vec{i}&\vec{j}&\vec{k}\\2&-1&2\\1&2&-1\end {vmatrix}= \vec{i}+2 \vec{j}+4 \vec{k}+\vec{k}-4 \vec{i}+2 \vec{j}=-3 \vec{i}+4 \vec{j}+5\vec{k}[/m]
[m]\vec{q}=(-3;4;5)[/m]
Уравнение прямой как прямой, проходящей через точку (х_(о); у_(о); z_(o)) c направляющим вектором [m]\vec{q}=(-3;4;5)[/m]
имеет вид:
[m]\frac{x-x_{o}}{-3}=\frac{y-y_{o}}{4}=\frac{z-z_{o}}{5}[/m]
Осталось найти точку
Линия пересечения плоскостей содержит бесчисленное множество точек.
В том числе там есть точка, у которой, например, z=0
Тогда из системы найдем х и у
[m]\left\{\begin {matrix}2x-y-3=0\\x+2y-1=0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}4x-2y-6=0\\x+2y-1=0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}5x-7=0\\x+2y-1=0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}x=\frac{7}{5}\\y=-\frac{2}{10}\end {matrix}\right.[/m]
[m]\frac{x-\frac{7}{5}}{-3}=\frac{y-(-\frac{2}{10})}{4}=\frac{z-0}{5}[/m]