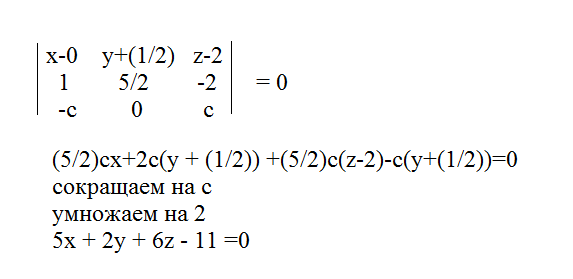Задача 32649 составить уравнение плоскости проходящей...

vk276969520

2019-01-11 11:33:32

составить уравнение плоскости проходящей через линию пересечения плоскостей х+2у+3z-5=0 и 3х-2у-z+1=0 и отсекающей равные отрезки на осях Ох и Оz

sova

2019-01-11 22:12:08

найдем две точки на линии пересечения плоскостей.

пусть х=0
{2y+3z-5=0
{-2y-z+1=0
cкладываем
2z-4=0
z=2
y=-1/2
К(0;-1/2;2)

пусть z=0
{x+2y-5=0
{3x-2y+1=0
складываем
4х-4=0
х=1
у=2
N(1;2;0)

Координаты точек, отсекающих равные отрезки на осях Ох и Оz:
P(c;0;0) и Q(0;0;c)

Cоставим уравнение плоскости
Пусть М(х;у;z) - произвольная точка плоскости.
Тогда векторы
vector{KM}=(x- 0;y+(1/2);z-2);
vector{KN}=(1;5/2;-2)
vector{PQ}=(-c;0;c) компланарны
Условием компланарности трех векторов является равенство 0 определителя третьего порядка, составленного из координат этих векторов.