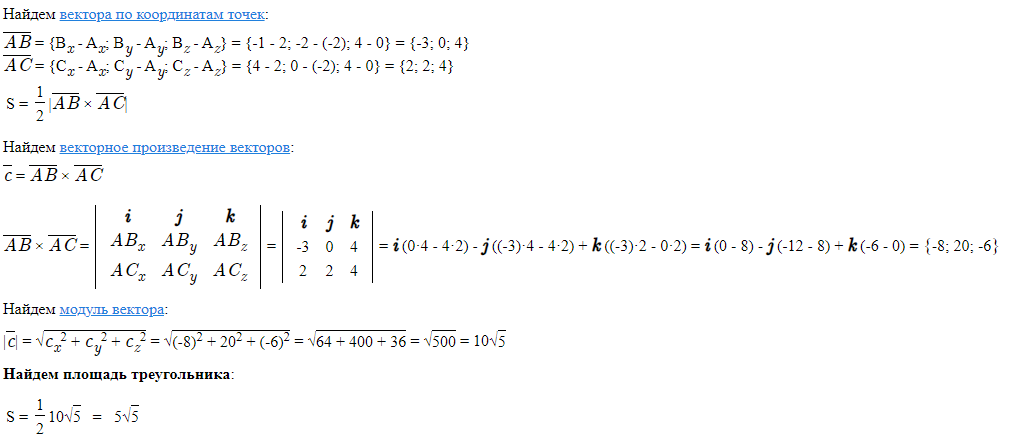Задача 57280 ...

5ff6f1fb960c3c35933da1c1

22.01.2021 18:31:01

1. Найти площадь ∆ABC и угол в точке A, если координаты точек
A(-2,-2,0), B(-1,-2,4), C(4,0,4)

2. Составить уравнение плоскости, проходящей через начало координат и перпендикулярно к вектору AB. если A(5,-2,3), B(1,-3,5).

5f3ea7e3faf909182968ddd9

22.01.2021 18:33:14

★

2)

Пусть M (x;y;z) - произвольная точка плоскости

Тогда vector{OM}=(x-0;y-0;z-0) лежит в плоскости

vector{AB}=(-3;0;4) - направляющий вектор плоскости

Значит, уравнение получим из условия ортогональности двух векторов


-3*(x-0)+0*(y-0)+4(z-0)=0

[b]-3x+4z=0[/b]


1)