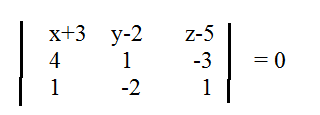Задача 32021 Провести плоскость через перпендикуляры,...

vk247797756

17 декабря 2018 г. в 15:22

Провести плоскость через перпендикуляры, опущенные из точки A(–3;2;5) на плоскости 4x+y–3z+13=0 b x–2y+z–11=0

sova

17 декабря 2018 г. в 15:39

★

Пусть М(х;у;z) – произвольная точка плоскости
Тогда
AM=(x+3;y–2;z–5)
n₁=(4;1;–3)
n₂=(1;–2;1)

компланарны.
Условие компланарности – равенство 0 смешанного произведения векторов.


О т в е т. (х+3)–3·(y–2)–8·(z–5)–(z–5)–6·(x+3)–4·(y–2)=0
–5·(x+3)–7·(y–2)–9·(z–5)=0
5x+7y+9z–44=0