Задача 67315 уравнение плоскости проходящей через...
Условие
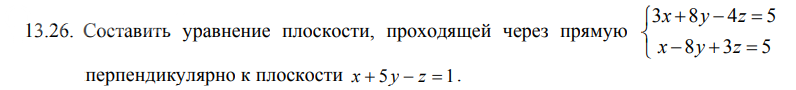
Решение
{3x+8y-4z=5
{x-8y+3z=5
3x+8y-4z=5 – общее уравнение плоскости с нормальным вектором vector{n_(1)}=(3;8;-4)
x-8y+3z=5 – общее уравнение плоскости с нормальным вектором vector{n_(2)}=(1;-8;3)
Направляющий вектор прямой [m]l[/m]
vector{q}=vector{n_(1)} × vector{n_(2)}
Находим векторное произведение векторов. заданных координатами:
vector{q}=vector{n_(1)} × vector{n_(2)}=[m]\begin {vmatrix} \vec{i}&\vec{j}&\vec{k}\\3&8&-4\\1&-8&3\end {vmatrix}=24\vec{i}-4\vec{j}-24\vec{k}-8\vec{k}+32\vec{i}-9\vec{j}=56\vec{i}-13\vec{j}-32\vec{k}[/m]
vector{q}=(56;-13;-32)
Искомая плоскость проходит через прямую, значит вектор vector{q} принадлежит искомой плоскости
x+5y-z=1 – общее уравнение плоскости с нормальным вектором vector{n}=(1;5;-1)
Искомая плоскость перпендикулярна плоскости, значит vector{n} параллелен плоскости.
Осталось найти точку, принадлежащую прямой [m]l[/m]
Так как прямая [m]l[/m] - линия пересечения плоскостей:
{3x+8y-4z=5
{x-8y+3z=5
то точек на ней - много.
Пусть у точки[b] z=0[/b]
тогда из системы
{3x+8y=5
{x-8y=5
находим две другие координаты
{3x+x-5=5 ⇒ 4x=10;[b] x=2,5[/b]
{x-5=8y
y=-25/80=[b]-5/16[/b]
[b]А(-2,5; -5/16; 0)[/b]
Пусть М (x;y;z) - произвольная точка искомой плоскости
Тогда векторы
vector{AM}=(х+2,5; y+(5/16); z-0)
vector{q}=(56;-13;-32)
vector{n}=(1;5;-1)
КОМПЛАНАРНЫ
Условие компланарности трех векторов - равенство нулю определителя третьего порядка, составленного из координат этих векторов
[m]\begin {vmatrix} x+2,5&y+\frac{5}{16}&z\\56&-13&-32\\1&5&-1\end {vmatrix}=0[/m]
Раскрываем определитель по правилу треугольника и получаем ответ