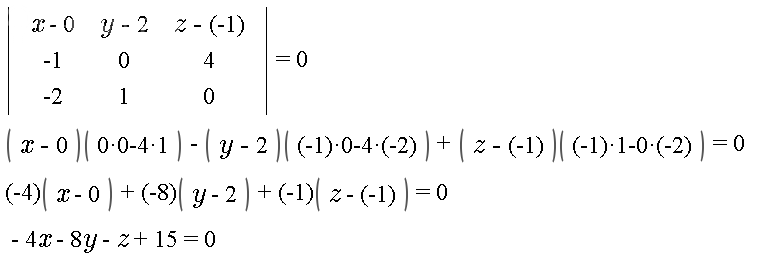Задача 66446 ...
Условие
перпендикулярно вектору
BC
. Написать ее общее уравнение, а также
нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить
уравнение плоскости
P1
, проходящей через точки А, В, С. Найти угол между
плоскостями Р и
P1
. Найти расстояние от точки D до плоскости Р
А(0;2;-1) В(-1;2;3) С(-2;3;-1) D(0;4;1)
Решение
плоскость Р ⊥ вектору vector{BC}
Значит,
vector{n}=vector{BC}=([green]-1[/green];[green]1[/green];[green]-4[/green])- нормальный вектор плоскости Р
Уравнение плоскости Р:
А([red]0[/red];[red]2[/red];[red]–1[/red])
([green]-1[/green])*(x-[red]0[/red])+[green]1[/green]*(y-[red]2[/red])+([green]-4[/green])*(z-([red]-1[/red]))=0
-x +y-2-4z-4=0
x-y+4z+6=0 -[i]общее уравнение плоскости[/i] Р
|vector{n}|=sqrt((-1)^2+1^2+(-4)^2)=sqrt(18)=3sqrt(2)
нормальное уравнение плоскости:
-x +y-4z-6=0 делим на |vector{n}|=3sqrt(2)
x/(-3sqrt(2)) + y/(3sqrt(2))-(4z)/(3sqrt(2))-6/(3sqrt(2))=0
x*сos α +y*cos β +z*cos γ -p=0
сos α=1/(-3sqrt(2))
cos β =1/(3sqrt(2))
cos γ =(4/(-3sqrt(2))
p=6/(3sqrt(2))
уравнение плоскости в отрезках
-x +y-4z-6=0
-x +y-4z=6
Делим на 6
(-1/6)x+(1/6)y-(4/6)z=1
(x/(-6)) + (y/6)+ (x/(-3/2))=1 -уравнение плоскости в отрезках
2.
Пусть M(x;y;z) - произвольная точка плоскости Р_(1)
Тогда векторы
vector{AM}=(x-0;y-2;z-(-1))=(x;y-2;z+1)
vector{AB}=(-1-0;2-2;3-(-1))=(-1;0;4)
vector{AC}=(-2-0;3-2;-1-(-1))=(-2;1;0)
КОМПЛАНАРНЫ, лежат в одной плоскости.
Значит , определитель третьего порядка, составленный из координат этих векторов равен 0 ( объем пирамиды АВСМ равен 0)