Задача 32448 Найдите острый угол между прямой [b]...

marat2015

26 декабря 2018 г. в 09:52

Найдите острый угол между прямой (x=t–1 y=–t+2 z= √2t) и плоскостью x+y+ √2z+5=0

sova

26 декабря 2018 г. в 14:00

★

Угол между прямой и плоскостью – угол между прямой и проекцией ее на плоскость
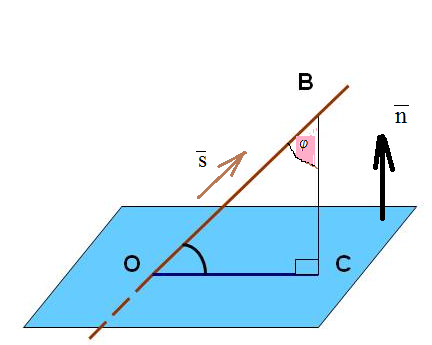
Легко найти угол между направляющим вектором прямой и нормальным вектором плоскости.

Нормальный вектор плоскости n=(1;1;√2)
Запишем уравнение прямой в каноническом виде.
Для этого выразим t
t=x–1;
t=(y–2)/(–1)
t=z/√2

(x–1)/1=(y–2)/(–1)=z/√2
Направляющий вектор прямой:
s=(1;–1;√2)

cos φ =cos ∠ (n,s)=

=n·s/(|n|·|s|=

=(1·1+1·(–1)+√2·√2)/√1+1+2·√1+2+2=2/4=1/2

φ=∠ (n,s)= arccos(1/2)=60^o

Искомый угол – угол, который дополняет найденный до 90^o

О т в е т.

90^o–60^o=30^o