Задача 32160 Найти проекцию точки М(1,4,3) на...

yanabas

2018-12-20 00:20:01

Найти проекцию точки М(1,4,3) на плоскость 3x – y + 2z + 9 = 0.

Введите координаты x0, y0, z0 проекции точки в указанном порядке.

sova

2018-12-20 07:32:46

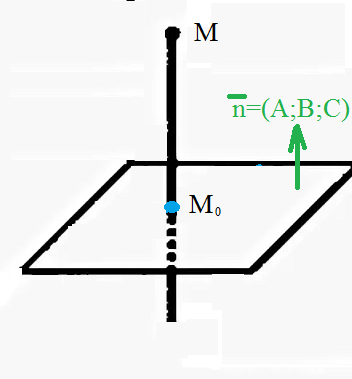
Составляем уравнение прямой, перпендикулярной данной плоскости и проходящей через точку М

Это значит, что направляющим вектором прямой является нормальный вектор плоскости.

vector{n}=(3;-1;2)

(x-1)/(3)=(y-4)/(-1)=(z-3)/2

Запишем это уравнение в параметрическом виде:

(x-1)/(3)=(y-4)/(-1)=(z-3)/2=t
x=3t+1
y=-t+4
z=2t+3

Найдем точку пересечения прямой и плоскости
Подставляем параметрические уравнения прямой
в уравнение плоскости

3*(3t+1) - (- t + 4) + 2* (2t+3) + 9 = 0

t= -1
При t= -1
x= - 3*(-1)+1= 4
y= - ( -1)+4 = 5
z=2*(-1) + 3 = 1
M_(o) (4;5;1) - проекция точки M на плоскость.

О т в е т. х_(о)=4; у_(о)=5; z_(o)=1