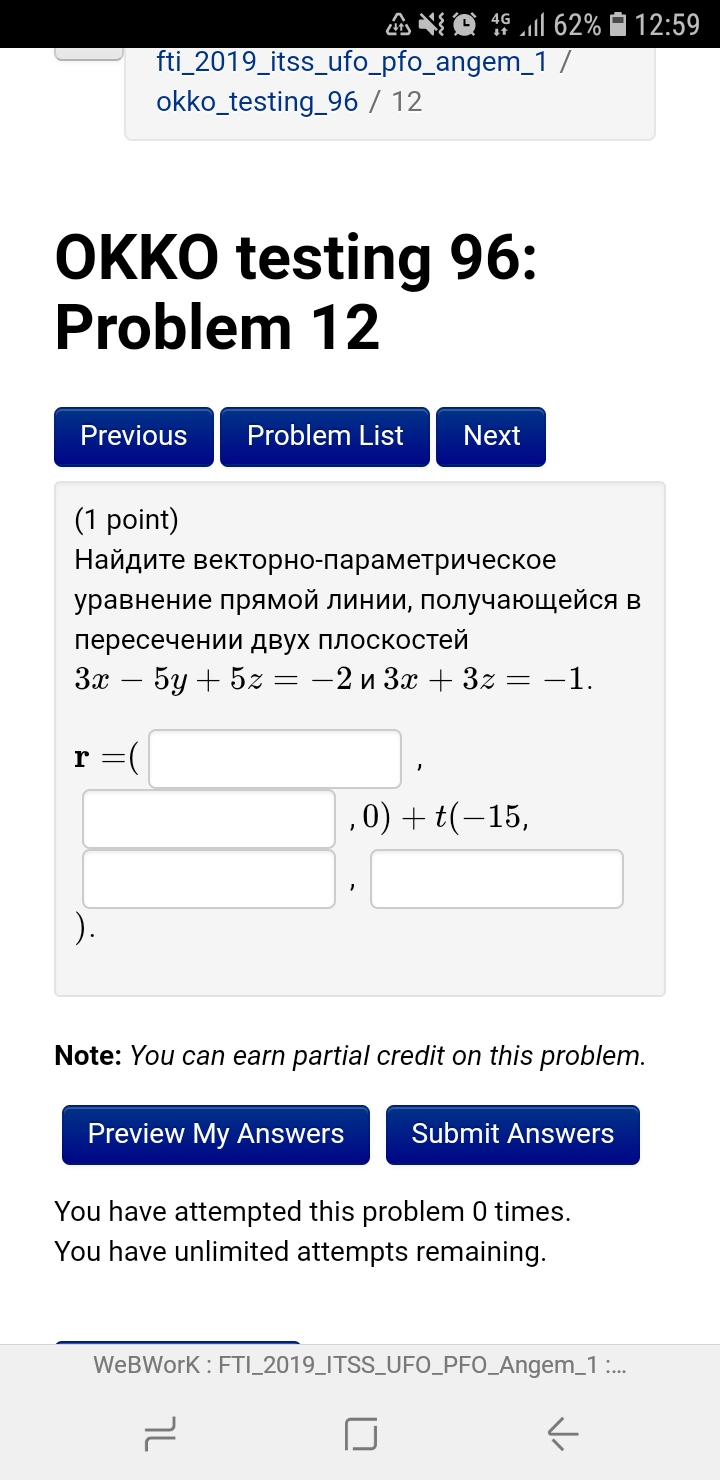
Задача 32876 Найдите векторно-параметрическое...

vk151256823

21 января 2019 г. в 10:54

Найдите векторно–параметрическое уравнение прямой линии, получающейся в пересечении двух плоскостей
3x – 5y + 5z = – 2 и 3x + 3z = – 1.

sova

21 января 2019 г. в 11:40

★

Найдем координаты двух точек, принадлежащих линии пересечения плоскостей
Решаем систему
{3x–5y+5z=–2
{3x+3z=–1
Система имеет бесчисленное множество решений.

По условию третья координата точки M_o
z=0
{3x–5y=–2
{3x=–1
x=(–1/3)
y=1/5

М_о(–1/3;1/5;0)

По условию первая координата M_oM=a
равна (–15)
значит
x_M–x_Mo=–15
x_M=–46/3

{3·(–46/3) –5y+5z=–2
{3·(–46/3)+3z=–1

z=15
5y=31
y=6,2

M(–46/3; 6,2; 15)
a=(–15; 6; 15)

r=r_o + t·a=

=(–1/3;1/5;0)+ t·(–15; 6; 15)

x=x(t)=(–1/3) – 15t
y=y(t)=(1/5) + 6t
z=z(t)=0 + 15t