Задача 32587 Известна точка пересечения диагоналей...

jakson

8 января 2019 г. в 15:42

Известна точка пересечения диагоналей квадрата K(1,5; 2,5) и уравнение одной из его сторон х–4у=0 . Найти координаты вершин квадрата и составить уравнения его диагоналей

sova

8 января 2019 г. в 17:42

★

Уравнение стороны запишем в виде уравнения с угловым коэффициентом:
y=(1/4)x
k=1/4
tg α =1/4
Тогда
уравнение диагонали:
y=k₁x+b
tg β =k₁

β – α =45^o
( диагонали квадрата образуют угол 45 ° со сторонами квадрата)
tg( β – α )=(tg β –tg α )/(1+tg β ·tg α )

(k₁–(1/4))/(1+(1/4)·k₁)=1

k₁=5/3


y=(5/3)x+b – уравнение диагонали

Подставим координаты точки К (1,5; 2,5)

2,5=(5/3)·1,5+b
b=0
y=(5/3)x

Диагонали взаимно перпендикулярны.
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (–1)

Значит уравнение второй диагонали
y=(–3/5)x+b

(–3/5)·(5/3)=–1

Подставим координаты точки К
2,5=(–3/5)·1,5+b
b=3,4

Координаты одной вершины получим как координаты точки пересечения стороны х–4у=0 и диагонали у=(5/3)х
Это точка (0;0)
{х–4у=0
{у=(5/3)х
x=0
y=0

Координаты второй вершины получим как координаты точки пересечения стороны х–4у=0 и диагонали у=(–3/5)х+3,4
{х–4у=0
{у=(–3/5)х+3,4

x=4
y=1

Координаты двух других точек можно найти из соображений симметрии.

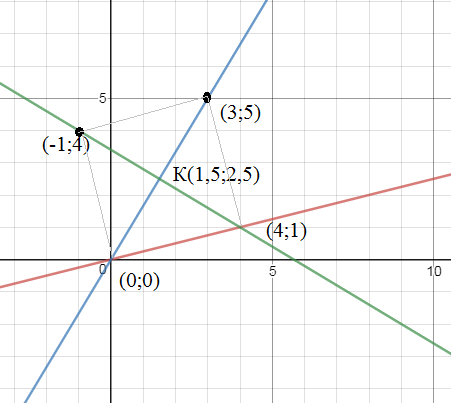
О т в е т. (0;0); (4;1);(–1;4);(3;5)