Задача 41766 ...

globaiv

2019-11-21 09:26:49

Установить, какую кривую определяет данное уравнение.
Найти:
1) координаты еѐ центра С;
2) полуоси;
3) координаты фокусов;
4) эксцентриситет;
5) уравнение директрисы;
6) уравнение асимптот (для гиперболы).
X2-4y2+6x+32y-119=0

с решением

sova

2019-11-21 10:31:32

Группируем, чтобы выделить полные квадраты:
(x^2+6x)-(4y^2-32y)-119=0

(x^2+2*x*3+3^2)-3^2-4*(y^2-2*y*4+4^2)+4*4^2-119=0

(x+3)^2-4*(y-4)^2=64

Делим на 64

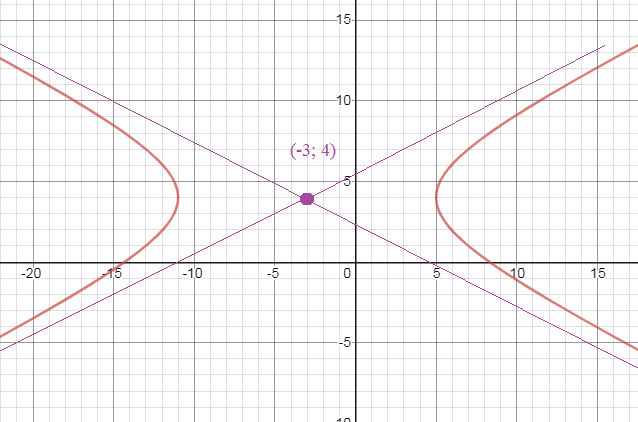
(x+3)^2/64 - (y-4)^2/16 = 1 - гипербола

c центром C(-3;4)
полуоси
a=8
b=4

c^2=a^2+b^2=64+16=80
c=sqrt(80)=sqrt(16*5)=4sqrt(5)

F(-4sqrt(5);4) и F(4sqrt(5);4) - фокусы

ε =с/a=4sqrt(5)/8=sqrt(5)/2

Для гиперболы
x^2/a^2+y^2/b^2=1

Асимптоты
y= ± (b/a)x

Для данной гиперболы
уравнения асимптот имеют вид:
y= ± (4/8)x + m

Асимптоты проходят через точку С.
Подставляем координаты точки С в уравнение:
y=- (1/2)x + m

4=-(1/2)*(-3)+m

m=2,5

Подставляем координаты точки С в уравнение:
y= (1/2)x + m

4=(1/2)*(-3)+m

m=5,5

О т в е т. [b]y= -0,5x+2,5[/b] и [b]y= 0,5x+5,5[/b]