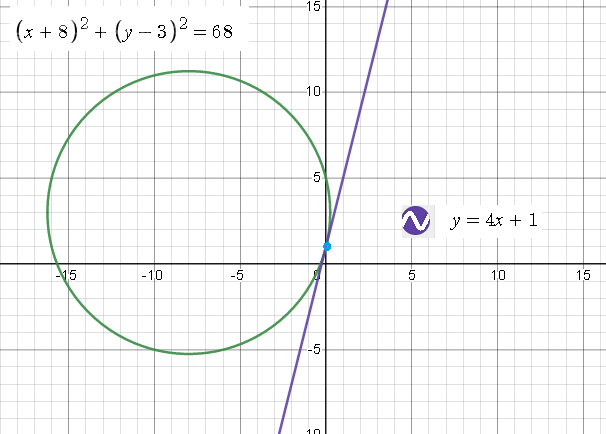
Задача 66571 Запишите уравнение касательной к...

635cefe051f9910430210751

29.10.2022 12:28:36

Запишите уравнение касательной к окружности(x+8)2+(y−3)2=68 в точке M0(0,1) в виде y=kx+d.
В ответ введите через точку с запятой значения:
k;d

5f3ea7e3faf909182968ddd9

29.10.2022 14:40:56

★

Касательная y=kx+d. имеет с окружностью одну общую точку
и проходит через точку (0;1)

Значит координаты этой точки точки удовлетворяют уравнению касательной

1=k*0+d ⇒ [blue]d=1[/blue]


Решаем систему уравнений

{(x+8)^2+(y−3)^2=68
{y=kx+1

Применяем способ подстановки:

{(x+8)^2+(kx+1−3)^2=68
{y=kx+1

Решаем первое уравнение:
(x+8)^2+(kx+1−3)^2=68
(x+8)^2+(kx−2)^2=68

x^2+16x+64+k^2x^2-4kx+4=68

(1+k^2)x^2+4(4-k)x=0

x*((1+k^2)x+4(4-k))=0

(1+k^2)x+4(4-k)=0 не должно иметь других корней кроме х=0

(1+k^2)*0+4*(4-k)=0 ⇒

k=4

[b]y=4x+1 - уравнение касательной[/b]