Задача 52474 составить каноническое уравнение...

pcdo908

16 июня 2020 г. в 08:47

составить каноническое уравнение гиперболы имеющих общие фокальные хорды с эллипсом x²/6+y²/4=1

sova

16 июня 2020 г. в 14:26

★

Для эллипса:

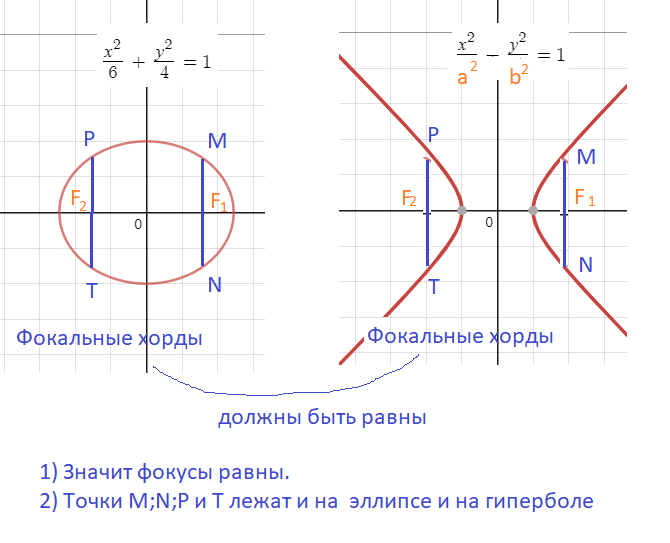
$\frac{x^2}{6}+\frac{y^2}{4}=1$ ⇒ a²=6; b²=4 ⇒ c²=a²–b²=2

F₂(–√2;0); F₁(√2;0) – фокусы эллипса.

Если x=√2 ⇒ $\frac{y^2}{4}=1-\frac{2}{6}$ ⇒ y= ± $\sqrt{\frac{8}{3}}$

M(√2; $\sqrt{\frac{8}{3}}$)

N(√2; $- \sqrt{\frac{8}{3}}$)

P(–√2; $\sqrt{\frac{8}{3}}$)
T(–√2; $- \sqrt{\frac{8}{3}}$)


Уравнение гиперболы:

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
b²=c²–a²

так как фокусы эллипса и гиперболы совпадают, то с²=2
⇒ b²+a²=2


Подставляем координаты точки M в каноническое уравнение гиперболы:
$\frac{2}{a^2}-\frac{\frac{8}{3}}{b^2}=1$ ⇒ 6b²–8a²=3a²b²

Из системы уравнений:
{b²+a²=2 ⇒ b²=2–a²
{6b²–8a²=3a²b² ⇒ 6·(2–a²)–8a²=3a²·(2–a²) ⇒

Биквадратное уравнение:

3a⁴–20a²+12=0
D=400–4·3·12=256
a²=6 или a²=(2/3)

b²=2–a²=2–6 < 0 или b²=2–(2/3)=4/3


$\frac{x^2}{\frac{2}{3}}-\frac{y^2}{\frac{4}{3}}=1$