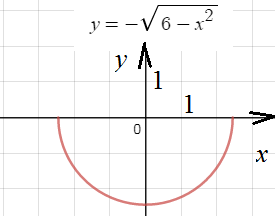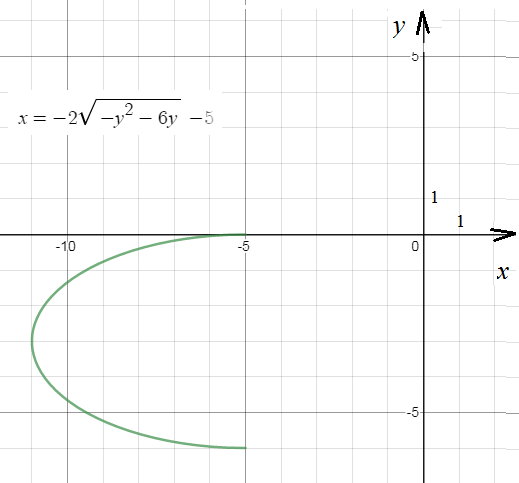Задача 41730 Изобразить линии:...
Условие
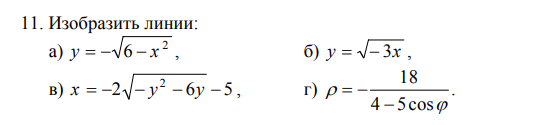
Все решения
y^2=6-x^2 ⇒ x^2+y^2=6 - окружность с центром (0;0), R=sqrt(6),
y=-sqrt(6-x^2) полуокружность,расположенная в нижней полуплоскости,[red] y ≤ 0[/red]
2)
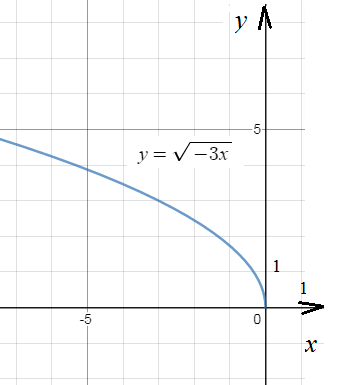
y^2=-3x - парабола
y=sqrt(-3x) - часть параболы y^2=-3x, расположенная в верхней полуплоскости
[red]y ≥ 0[/red]
3)
x+5=-2sqrt(-y^2-6y)
(x+5)^2=4(-y^2-6y)
Выделяем полный квадрат
(x+5)^2=4(-y^2-6y-9)+36
(x+5)^2+4(y+3)^2=36
Делим на 36:
((x+5)^2/36)+((y+3)^2/9)=1 - эллипс с центром (-5;-3) и полусями
а=6
b=3
4.
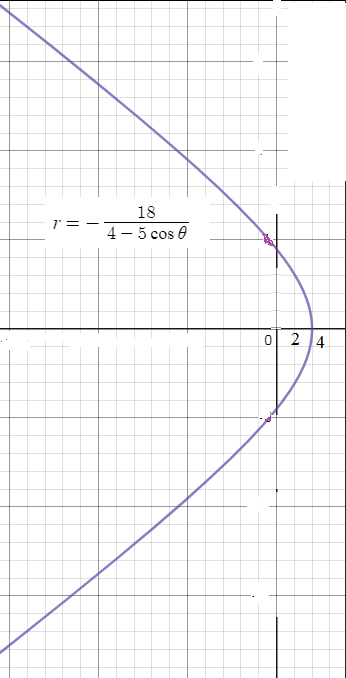
ρ =sqrt(x^2+y^2)
cos φ =x/ ρ =x/sqrt(x^2+y^2)
sqrt(x^2+y^2)= - 18/(4-(5х/sqrt(x^2+y^2)))
4sqrt(x^2+y^2)=5x-19
16*(x^2+y^2)=25x^2-190x+361 - выделяем полный квадрат, получим уравнение гиперболы
График - одна ее ветвь