О категории
Переход от декартовой к полярной и обратно. Построение графиков в полярной системе координат
Практика (32)
Доброго времени суток!
Даны уравнения линий в полярной системе координат.
Вар. 4.2. r = 6/(1–cosφ)
Требуется:
1) Построить линию на промежутке от φ=0 до φ=2π с шагом, равным π/8.
2) Найти уравнение линии в прямоугольной декартовой системе координат и назвать линию.
в полярной системе координат даны точки а (8 -2\3*п) и в (6 п\3). Найти полярные координаты середины отрезка, соединяющего эти точки
построить Кривую p=5sin2a
Найти уравнение кривой (х^2 + у^2)^2 =2у^2 в полярной системе координат. Построить кривую.
Задача 22. Записать уравнения в полярных координатах и построить кривые: х = —1, у=8, у+х = —3, х^+ у^ = 10, х^ + у^ =х, х^+ у^= —2у
ИДЗ №6 «Кривые второго порядка. Полярная система координат» 1) Постройте кривые в полярной системе координат по точкам, давая значения л через промежуток —. ‚ начиная от ф =0. 2) Найдите уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абецисс — ¢ полярной осью и по уравнению определите вид кривой.
Линия задана уравнением r = r(фи) в полярной системе координат.
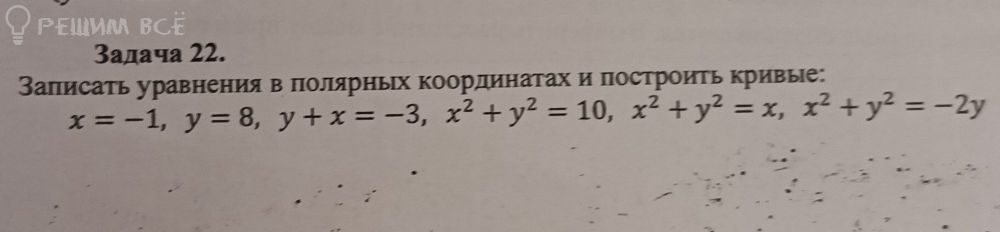
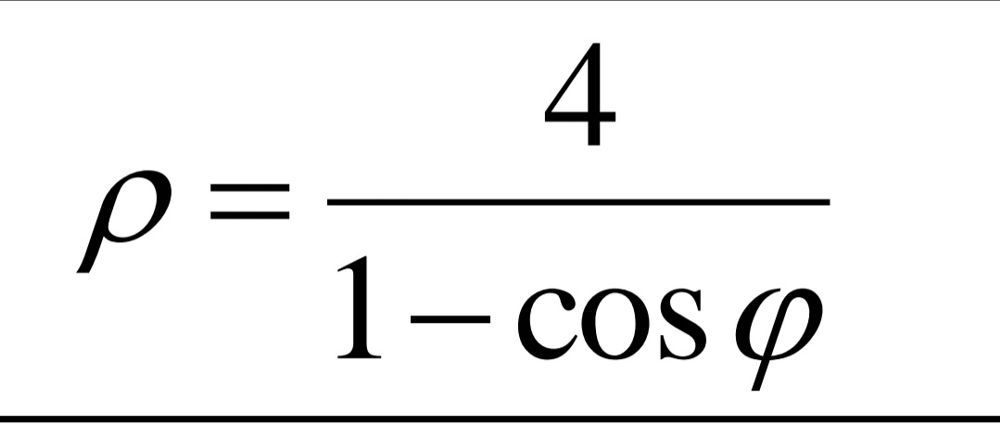
Требуется:
1) построить линию по точкам от фи=0 до фи =пи , придавая значения через промежуток пи/6;
2) найти уравнение линии в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось OX - с
полярной осью;
3) определить вид линии по уравнению в декартовой системе координат;
4) сделать чертеж.
Перейти в уравнение кривой к полярным координатам и построить кривую
По полярным координатам точек: ???? (2,
????
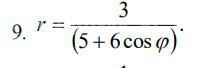
3
); ???? (√2,
3????
4
); ???? (5,
????
2
); ???? (3, −
????
6
)
определить их прямоугольные декартовы координаты.
Линия задана уравнением ρ = cos ϕ − sin ϕ в полярной системе координат. Требуется:
1) построить линию по точкам, придавая ϕ значения через промежуток
π/4;
2) найти уравнение кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось Ox – с полярной осью
7. Постройте кривую, заданную уравнением в полярной системе координат
ρ = 2 sin 4φ.
Полярная ось полярной системы координат параллельна оси абсцисс декартовой системы координат и направлена одинаково с нею. Декартовы прямоугольные координаты полюса О(0;0). Определите координаты точки M в полярной системе координат, если...
перевести в поляную систему уравнения х2+у2=2Ry
Записать уравнения кривых в полярной системе координат = (x²+y²)³ = 4(x²+2y²) , при x=cosφ * ρ , y = sinφ * ρ
Ребят здесь алгебра и геометрия
Линия задана уравнением ρ = ρ(ϕ) в полярной системе координат. Требуется:
1) построить линию по точкам, придавая ϕ значения через промежуток
π/4;
2) найти уравнение кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полуось Ox – с полярной осью.
ρ = 3(1 + 2 sin ϕ).
1)найти площадь фигуры ограниченной линией p=4sin(2φ )
2)Найти обьем тела полученного вращением вокруг оси Оγ фигуры, ограниченной линиями y^2=9-x, x=0 .
C решением
Изобразить линии:
Уравнение кривой r=3cosu преобразовать к декартовым координатам найти основные параметры кривой и построить ее
Построить кривую, заданную в полярных координатах
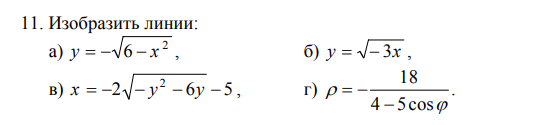
r=3,5*(1-cos φ )
дан правильный треугольник ABC сторона которого равна 5 приняв вершину A за полюс полярной системы координат а направленную прямую AB за полярную ось определить полярные координаты вершин ицентра P треугольника Рассмотреть два возможных случая расположения треугольника относительно полярной осн
дан правильной шестиугольник FBCDEF строна которого равна a приняв точку A за полюс а направленную прямую AB за ось полярной системы координат определить координаты всех его вершин и точки Р пересечения
диагоналей Рассмотреть два возможных случая расположения шестиугольника относительно полярной осн.
Перейти к полярным координатам и построить кривую
(x^2+y^2)^2 = -6xy
Дано уравнение линии [m]\rho = f(\varphi)[/m] в полярной системе координат. Определить точки, лежащие на линии, в промежутке [m]0 \leq \varphi \leq 2\pi[/m]. Шаг взять равным [m]\pi/8[/m]. Построить линию. Записать уравнение линии в декартовой системе координат.
14. [m]\rho = \frac{4}{2 + \sin \varphi}[/m].
Построить кривую, заданную уравнением в полярной системе координат
p=2cos6φ
1) Найти полярные координаты точек, симметричных точкам (2;pi/4), (1;-pi/3), (3;0) относительно
а)полюса
б)полярной оси
2) треугольник авс задан полярными координатами вершин А(5;pi/2), B(8;5pi/6) C(3;7pi/6). Доказать, что треугольник равнобедренный.
Задана линия своим уравнением в полярной системе координат. Необходимо: 1)
определить точки, лежащие на линии, придавая j значения через промежуток,
равный p/8, начиная от j = 0 и до j = 2p; 2) построить линию, соединив
полученные точки; 3) найти уравнение этой линии в прямоугольной декартовой
системе координат.
p =5 /(3 - 4 *sin φ)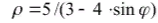
а) построить по точкам в полярной системе координат кривые (r больше или равно 0)
б) перейдя к полярной системе координат, построить кривые.
а) r = 3sin2φ
б) 4(x^2+y^2-x)^2 = 9(x^2+y^2)
II. Требуется: 1) построить по точкам график функции [m] p = p(\phi) [/m] в полярной системе координат. Значения функции вычислить в точках [m] \phi = \pi k/8 [/m]; 2) найти уравнение кривой в прямоугольной системе координат, начало которой совмещено с полюсом, а положительная полюс Ox — с полярной осью; 3) определить вид кривой.
[m] p = 4 \sin \phi [/m].
Перейти в уравнение кривой к полярным координатам и построить кривую
Дано уравнение линии ρ = f(φ) в полярной системе координат. Определить точки, лежащие на линии, в промежутке 0 ≤ φ ≤ 2π. Шаг взять равным π/8. Построить линию. Записать уравнение линии в декартовой системе координат.
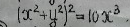
16. ρ = 2/(2 - cosφ) .
Редакторы (1)
SOVA